题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() .
.
(Ⅰ)求曲线![]() 被直线
被直线![]() 截得的弦长;
截得的弦长;
(Ⅱ)与直线![]() 垂直的直线
垂直的直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,求点
,求点![]() 的直角坐标.
的直角坐标.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ) 或
或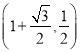 .
.
【解析】
(Ⅰ)首先把极坐标方程和直角坐标方程之间进行转换,进一步利用点到直线的距离公式和勾股定理的应用求出弦长.
(Ⅱ)利用直线垂直的充要条件的应用求出圆的切线方程,进一步利用直线和曲线的位置关系的应用求出切点的直角坐标.
(Ⅰ)由题意,曲线![]() ,可得
,可得![]() ,
,
又由![]() ,可得曲线的直角坐标方程为
,可得曲线的直角坐标方程为![]() ,
,
即![]() ,其中圆心坐标为
,其中圆心坐标为![]() ,半径为1,
,半径为1,
所以圆心![]() 到直线
到直线![]() 的距离
的距离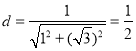 ,
,
所以曲线![]() 被直线
被直线![]() 截得的弦长为
截得的弦长为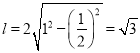 .
.
(Ⅱ)因为直线![]() 与直线
与直线![]() 垂直,设直线
垂直,设直线![]() 的方程为
的方程为![]() ,
,
由直线![]() 与曲线
与曲线![]() 相切,可得圆心
相切,可得圆心![]() 到直线
到直线![]() 的距离
的距离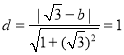 ,
,
解得![]() 或
或![]() ,
,
所以直线![]() 的方程为
的方程为![]() 或
或![]() .
.
设切点![]() ,联立方程组
,联立方程组 ,解得
,解得 ,
,
方程组 ,解得
,解得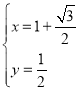 ,
,
即切点坐标为 或
或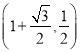 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目