题目内容
【题目】已知函数
．
（1）当
=0时，求实数的m值及曲线
在点（1， 
）处的切线方程；
（2）讨论函数
的单调性．
【答案】（1）m=﹣1,y=﹣1（2）见解析
【解析】试题分析：（1）求出
,由
的值可得切点坐标，求出
的值，可得切线斜率，利用点斜式可得曲线
在点
处的切线方程；（2）求出
，分四种情况讨论
的范围，在定义域内，分别令
求得
的范围，可得函数
增区间， 
求得
的范围，可得函数
的减区间；
求导，利用导数与函数单调性的关系，分类讨论
的取值范围，分别求得
单调区间.
试题解析：（1）函数y=f（x）的定义域为（0，+∞），
求导
，
由f'（1）=0，解得m=﹣1
从而f（1）=﹣1，曲线y=f（x）在点（1，f（1））处的切线方程为y=﹣1．
（2）由
，
当m≥0时，函数y=f（x）的减区间为（0，
），增区间为（，+∞）
当m＜0时，由
，得
，或
，
当m＜﹣2时，y=f（x）的减区间为（0，﹣
）和（，+∞）增区间为（﹣，）；
当m=﹣2时，y=f（x）的减区间为（0，+∞）没有增区间．
当﹣2＜m＜0时，y=f（x）的减区间为（0，
）和（﹣
，+∞），增区间为（，﹣）
综上可知：当m≥0时，函数y=f（x）的减区间为（0，），增区间为（，+∞）；
当m＜﹣2时，y=f（x）的减区间为（0，﹣）和（，+∞）增区间为（﹣，）；
当m=﹣2时，y=f（x）的减区间为（0，+∞）没有增区间；
当﹣2＜m＜0时，y=f（x）的减区间为（0，
）和（﹣
，+∞），增区间为（，﹣）．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】下表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费y（万元）的几组对照数据:
x（年） | 2 | 3 | 4 | 5 | 6 |
y（万元） | 1 | 2.5 | 3 | 4 | 4.5 |
（1）若知道y对x呈线性相关关系，请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
；
（2）已知该工厂技术改造前该型号设备使用10年的维修费用为9万元，试根据（1）求出的线性回归方程，预测该型号设备技术改造后，使用10年的维修费用能否比技术改造前降低?参考公式: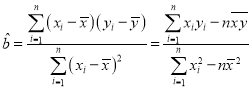
，
.
