题目内容
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() 、
、![]() ,
,![]() ,点
,点![]() 在椭圆上,且
在椭圆上,且![]() 的周长为
的周长为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 的坐标为
的坐标为![]() ,不过原点
,不过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,
,![]() ,
,![]() 三点共线,求
三点共线,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)根据焦距和焦点三角形周长可求得![]() ,利用
,利用![]() 求得
求得![]() ,从而可得椭圆的方程;(Ⅱ)当直线
,从而可得椭圆的方程;(Ⅱ)当直线![]() 斜率不存在时,可判断出
斜率不存在时,可判断出![]() ,
,![]() ,
,![]() 三点不共线,不符合题意;所以可假设出直线方程,与椭圆方程联立,利用韦达定理表示出
三点不共线,不符合题意;所以可假设出直线方程,与椭圆方程联立,利用韦达定理表示出![]() 和
和![]() ;由三点共线得到斜率相等关系,从而可求得
;由三点共线得到斜率相等关系,从而可求得![]() ;利用弦长公式和点到直线距离公式求得
;利用弦长公式和点到直线距离公式求得![]() 和
和![]() ,代入可整理出:
,代入可整理出: ,可知当
,可知当![]() 时取最大值.
时取最大值.
(Ⅰ)由题意得:![]() ,
,![]()
解得:![]() ,
,![]()
![]()
![]() 椭圆
椭圆![]() 的方程为
的方程为![]()
(Ⅱ)设![]() ,
,![]()
当直线![]() 与
与![]() 轴垂直时,由椭圆的对称性可知,点
轴垂直时,由椭圆的对称性可知,点![]() 在
在![]() 轴上,且与
轴上,且与![]() 点不重合
点不重合
显然![]() ,
,![]() ,
,![]() 三点不共线,不符合题设条件
三点不共线,不符合题设条件
故可设直线![]() 的方程
的方程![]()
由![]() ,消去
,消去![]() 整理得:
整理得:![]() ……①
……①
则![]()
![]() ,
,![]()
![]() 点
点![]() 的坐标为
的坐标为![]()
![]() ,
,![]() ,
,![]() 三点共线
三点共线 ![]()

![]()
![]()
此时方程①为:![]() ,则
,则![]()
![]()
则![]() ,
,![]()
![]()
又![]()
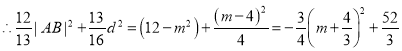
![]() 当
当![]() 时,
时,![]() 的最大值为
的最大值为![]()

【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 与直线
与直线![]() 的直角坐标方程.
的直角坐标方程.
(2)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,
,![]() ,求
,求![]() 的值.
的值.
【题目】随着手机的发展,“微信”逐渐成为人们支付购物的一种形式.某机构对“使用微信支付”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信支付”赞成人数如下表.
年龄 (单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄45岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信支付”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信支付”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在![]() 的被调查人中按照赞成与不赞成分层抽样,抽取5人进行追踪调查,在5人中抽取3人做专访,求3人中不赞成使用微信支付的人数的分布列和期望值.
的被调查人中按照赞成与不赞成分层抽样,抽取5人进行追踪调查,在5人中抽取3人做专访,求3人中不赞成使用微信支付的人数的分布列和期望值.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
【题目】某校为了推动数学教学方法的改革,学校将高一年级部分生源情况基本相同的学生分成甲乙两个班,每班各40人,甲班按原有模式教学,乙班实施教学方法改革.经过一年的教学实验,将甲乙两个班学生一年来的数学成绩取平均数,两个班学生的平均成绩均在![]() ,按照区间
,按照区间![]() ,
,![]() ,
,![]() 进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
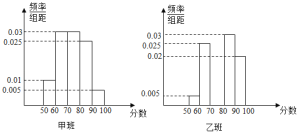
(1)完成表格,并判断是否有90%以上的把握认为“数学成绩优秀与教学改革有关”;
甲班 | 乙班 | 总计 | |
大于等于80分的人数 | |||
小于80分的人数 | |||
总计 |
(2)从乙班![]() 分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自
分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自![]() 发言的人数为随机变量
发言的人数为随机变量![]() ,求
,求![]() 的分布列和期望.附:
的分布列和期望.附: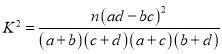 ,
,
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
