题目内容
【题目】已知线段AB的端点B的坐标是(4,2),端点A在圆C:(x+2)2+y2=16上运动.
(1)求线段AB的中点的轨迹方程H.
(2)判断(1)中轨迹H与圆C的位置关系.
(3)过点P(3,2)作两条相互垂直的直线MN,EF,分别交(1)中轨迹H于M,N和E,F,求四边形MNFE面积的最大值
【答案】(1)(x﹣1)2+(y﹣1)2=4.(2)两圆相交.(3)![]() .
.
【解析】
(1)设![]() ,
,![]() ,中点
,中点![]() ,根据已知关系,由相关点法即可得出圆
,根据已知关系,由相关点法即可得出圆![]() 的方程;
的方程;
(2)比较圆心距与两圆半径的关系,得出两圆位置关系;
(3)根据圆的完美性,本题把圆和点同时向左和向下平移一个单位后,就可以把问题转换为![]() 与圆
与圆![]() 的问题求解.
的问题求解.
(1)设A(x0,y0),中点H(x,y),
则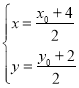 ,∴
,∴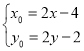 ,
,
代入圆C:(x+2)2+y2=16中,
化简得圆H:(x﹣1)2+(y﹣1)2=4;
(2)两圆圆心分别为C(﹣2,0),H(1,1),半径分别为![]() ,
,
∴圆心距d![]() ,
,
∴r1﹣r2<d<r1+r2
∴两圆相交;
(3)根据圆的完美性,本题把圆和点同时向左和向下平移一个单位后,
就可以把问题转换为(2,1)与圆x2+y2=4的问题,
为方便,点名均不变,则P(2,1),H(0,0),
记圆心H到直线MN,EF的距离分别为d1,d2,
则![]() ,r=2,
,r=2,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
所以四边形MNFE的面积为
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
又由![]() 可以得|x1x2+y1y2|
可以得|x1x2+y1y2|![]() ,
,
所以![]() ,
,
当且仅当d1=d2时取等号,
即四边形MNFE的面积最大为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
