题目内容
【题目】已知函数
（1）讨论函数
的单调性
（2）函数
，且
．若
在区间（0，2）内有零点，求实数m的取值范围
【答案】（1）见解析；
（2）
.
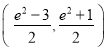【解析】
（1）f′（x）
ex﹣m，对m分类讨论，利用导数的正负研究函数的单调性即可得出．
（2）设
是
在区间
内的一个零点，由g（0）＝g（）＝g（2）＝0，转化为：
在区间内至少有两个不同零点
及
，通过研究
的单调性、极值最值，进而得出m的取值范围．
（1）f′（x）ex﹣m，
①当
时，
成立，
在
上单调递增；
②当
时，令
，得
，则在区间
单调递减，在
单调递增.
（2）
，
设是在区间内的一个零点，因为
，
，可知在区间
上不单调，故在区间存在零点；同理：由
，可知在区间
上存在零点，即在区间内至少有两个不同零点及.
由（1）知，
，得
，此时在区间
单调递减，在
单调递增.
由
，知
，
所以
，则
；
故只需：
，解得：
.
所以实数
的取值范围是.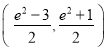
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
【题目】十三届全国人大二次会议于2019年3月5日在京召开.为了了解某校大学生对两会的关注程度，学校媒体在开幕后的第二天，从学生中随机抽取了180人，对是否收看2019年两会开幕会情况进行了问卷调查，统计数据得到列联表如下：
收看 | 没收看 | 合计 | |
男生 | 40 | ||
女生 | 30 | 60 | |
合计 |
（1）请完成列联表；
（2）根据上表说明，能否有99%的把握认为该校大学生收看开幕会与性别有关？（结果精确到0.001）
附：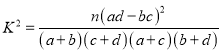
，其中
.
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
