题目内容
【题目】连接正方体每个面的中心构成一个正八面体,则该八面体的外接球与内切球体积之比为______.
【答案】![]() .
.
【解析】
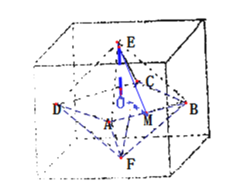
正八面体中ABCD四点或AFCE四点所组成的截面在外接球的一个大圆面上,可得其对角线的长度即为外接球的直径,又正方体中心设为O,取AB中点M,则在直角△OME中,斜边ME上的高即为内切球的半径,由此能求出结果.
若正八面体的外接球的各个顶点都在同一个球面上,
则其中ABCD四点或AFCE四点所组成的截面在球的一个大圆面上,
可得,此四点组成的正方形是球的大圆的一个内接正方形,
其对角线的长度即为球的直径,
设正八面体边长为2,且每个侧面三角形均为等边三角形,
故FE=AC=2![]() ,则外接球的半径是
,则外接球的半径是![]() ,
,
又正方体中心设为O,取AB中点M,则在直角△OME中,斜边ME=![]() =
=![]() ,
,
斜边ME上的高即为内切球的半径,大小为![]() =
=![]() ,
,
∴外接球与内切球半径之比为![]() ,∴外接球与内切球体积之比为
,∴外接球与内切球体积之比为![]()
故答案为![]() .
.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目