题目内容
12. 如图,在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,AB上的点C平分该弧.
如图,在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,AB上的点C平分该弧.(1)证明:平面POD⊥平面PAC;
(2)求二面角B-PA-C的余弦值.
分析 (1)连结OD,易得AC⊥OD,通过PO⊥底面⊙O可得AC⊥PO,利用线面垂直、面面垂直的判定定理即得结论;
(2)在平面POD中,过O作OH⊥PD于H,易知OH⊥平面PAC,进而可得PA⊥OH.在平面PAO中,过O作OG⊥PA于G,连结HG,则∠OGH为二面角B-PA-C的平面角.在Rt△ODA中计算可得OD=$\frac{\sqrt{2}}{2}$,在Rt△POD中计算可得OH=$\frac{\sqrt{10}}{5}$,在Rt△POA中计算可得OG=$\frac{\sqrt{6}}{3}$,在Rt△OHG中计算可得sin∠OGH=$\frac{\sqrt{15}}{5}$,进而由cos∠OGH=$\sqrt{1-sin2∠OGH}$计算即得结论.
解答 解:(1)连结OD,∵OA=OC,D是AC的中点,∴AC⊥OD,
又∵PO⊥底面⊙O,AC?底面⊙O,∴AC⊥PO,
∵OD、PO是平面POD内的两条相交直线,
∴AC⊥平面POD,
又∵AC?平面PAC,
∴平面POD⊥平面PAC;
(2)在平面POD中,过O作OH⊥PD于H,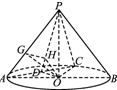
由(1)知,平面POD⊥平面PAC,∴OH⊥平面PAC,
又PA?面PAC,∴PA⊥OH.
在平面PAO中,过O作OG⊥PA于G,连结HG,
则有PA⊥平面OGH,从而PA⊥HG,
故∠OGH为二面角B-PA-C的平面角.
在Rt△ODA中,OD=OA•sin45°=1×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$,
在Rt△POD中,OH=$\frac{PO•OD}{\sqrt{P{O}^{2}+O{D}^{2}}}$=$\frac{\sqrt{2}×\frac{\sqrt{2}}{2}}{\sqrt{(\sqrt{2})^{2}+(\frac{\sqrt{2}}{2})^{2}}}$=$\frac{\sqrt{10}}{5}$.
在Rt△POA中,OG=$\frac{PO•OA}{\sqrt{P{O}^{2}+O{A}^{2}}}$=$\frac{\sqrt{2}×1}{\sqrt{2}+1}$=$\frac{\sqrt{6}}{3}$,
在Rt△OHG中,sin∠OGH=$\frac{OH}{OG}$=$\frac{\sqrt{10}}{5}$×$\frac{3}{\sqrt{6}}$=$\frac{\sqrt{15}}{5}$,
∴cos∠OGH=$\sqrt{1-sin2∠OGH}$=$\frac{\sqrt{10}}{5}$,
∴二面角B-PA-C的余弦值为$\frac{\sqrt{10}}{5}$.
点评 本题考查面面垂直的判定,考查求二面角的余弦值,注意解题方法的积累,属于中档题.

| A. | {x|-3<x≤-1} | B. | {x|-3≤x<-1} | C. | {x|-3≤x≤-1} | D. | {x|-3<x<-1} |
| A. | 1 | B. | $\sqrt{3}$+1 | C. | $\sqrt{3}$ | D. | 3 |
 已知棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,点P,Q分别在棱A1B1、A1D1上,且A1P=A1Q=x(0<x<1),设平面MEF∩平面MPQ=l,则下列结论中错误的是( )
已知棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,点P,Q分别在棱A1B1、A1D1上,且A1P=A1Q=x(0<x<1),设平面MEF∩平面MPQ=l,则下列结论中错误的是( )| A. | l∥平面ABCD | |
| B. | l⊥AC | |
| C. | 存在x0∈(0,1),使平面MEF与平面MPQ垂直 | |
| D. | 当x变化时,l是定直线 |
| A. | 4 | B. | 3 | C. | 2 | D. | 无数 |
| A. | [1,2] | B. | (1,2] | C. | (1,+∞) | D. | [2,+∞) |