题目内容
4.已知复数f(n)=in(n∈N*),则集合{z|z=f(n)}中元素的个数是( )| A. | 4 | B. | 3 | C. | 2 | D. | 无数 |
分析 直接利用复数的幂运算,化简求解即可.
解答 解:复数f(n)=in(n∈N*),可得f(n)=$\left\{\begin{array}{l}i,n=4k+1\\-1,n=4k+2\\-i,n=4k+3\\ 1,n=4k\end{array}\right.$,k∈Z.
集合{z|z=f(n)}中元素的个数是4个.
故选:A.
点评 本题考查复数单位的幂运算,基本知识的考查.

练习册系列答案
相关题目
14.设全集U=R,集合M={x|0<x≤1},N={x|x≤0},则M∩(∁UN)=( )
| A. | {x|0≤x<1} | B. | {x|0<x≤1} | C. | {x|0≤x≤1} | D. | {x|x<1} |
19.有4名优秀学生A,B,C,D全部被保送到甲,乙,丙3所学校,每所学校至少去一名,则不同的保送方案共有( )
| A. | 26种 | B. | 32种 | C. | 36种 | D. | 56种 |
16.已知全集U=R,若集合A={y|y=3-2-x},B={x|x=$\frac{x-2}{x}$≤0},则A∩(CUB)=( )
| A. | (-∞,0)∪[2,3) | B. | (-∞,0]∪(2,3) | C. | [0.2) | D. | [0.3) |
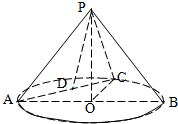 如图,在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,AB上的点C平分该弧.
如图,在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,AB上的点C平分该弧.