题目内容
设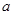 是一个自然数,
是一个自然数,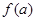 是
是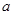 的各位数字的平方和,定义数列
的各位数字的平方和,定义数列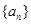 :
: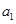 是自然数,
是自然数,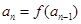 (
(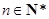 ,
,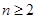 ).
).
(1)求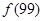 ,
,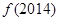 ;
;
(2)若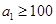 ,求证:
,求证: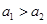 ;
;
(3)求证:存在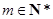 ,使得
,使得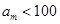 .
.
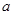 是一个自然数,
是一个自然数,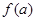 是
是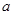 的各位数字的平方和,定义数列
的各位数字的平方和,定义数列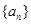 :
: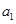 是自然数,
是自然数,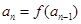 (
(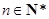 ,
,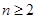 ).
).(1)求
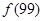 ,
,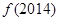 ;
;(2)若
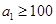 ,求证:
,求证: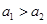 ;
;(3)求证:存在
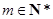 ,使得
,使得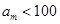 .
.(1)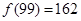 ,
,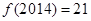 ;(2)证明过程详见解析;(3)证明过程详见解析.
;(2)证明过程详见解析;(3)证明过程详见解析.
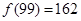 ,
,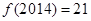 ;(2)证明过程详见解析;(3)证明过程详见解析.
;(2)证明过程详见解析;(3)证明过程详见解析.试题分析:本题是一道新定义题,主要考查归纳推理、数学归纳法、分类讨论思想等基础知识,考查学生的分析问题解决问题的能力和转化能力.第一问,由于
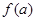 是a的各位数字的平方和,所以
是a的各位数字的平方和,所以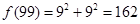 ,
,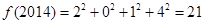 ;第二问,通过题干中给出的
;第二问,通过题干中给出的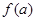 的定义设出
的定义设出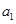 的值,利用
的值,利用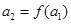 ,得到
,得到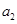 的值,然后用作差法比较
的值,然后用作差法比较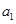 和
和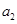 的大小;第三问,用反证法,先假设不存在
的大小;第三问,用反证法,先假设不存在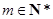 ,使得
,使得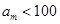 ,经过推理得出矛盾即可.
,经过推理得出矛盾即可.(1)
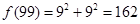 ;
;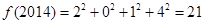 . 5分
. 5分(2)假设
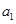 是一个
是一个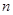 位数(
位数(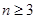 ),
),那么可以设
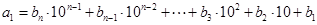 ,
,其中
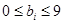 且
且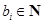 (
(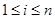 ),且
),且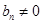 .
.由
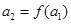 可得,
可得,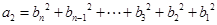 .
.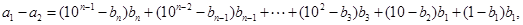
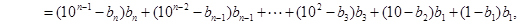
所以
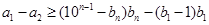 .
.因为
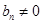 ,所以
,所以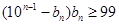 .
.而
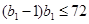 ,
,所以
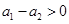 ,即
,即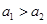 . 9分
. 9分(3)由(2)可知当
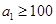 时,
时, 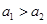 .
.同理当
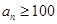 时,
时, 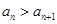 .
.若不存在
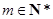 ,使得
,使得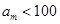 .
.则对任意的
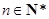 ,有
,有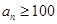 ,总有
,总有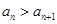 .
.则
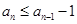 ,
,可得
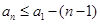 .
.取
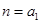 ,则
,则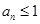 ,与
,与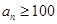 矛盾.
矛盾.存在
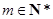 ,使得
,使得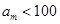 . 14分
. 14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
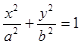 (
(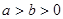 ),圆的标准方程
),圆的标准方程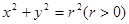 ,即
,即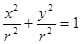 ,类比圆的面积
,类比圆的面积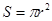 推理得椭圆的面积
推理得椭圆的面积 。
。
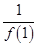 +
+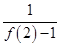 +
+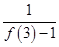 +…+
+…+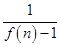 的值.
的值.



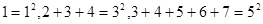 ,按此规律下去,第7个等式为 .
,按此规律下去,第7个等式为 .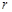 与它的高
与它的高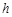 的关系是:
的关系是: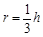 ,把这个结论推广到空间正四面体,则正四面体内切球的半径
,把这个结论推广到空间正四面体,则正四面体内切球的半径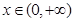 有下列各式:
有下列各式: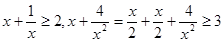 ,
,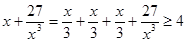 成立,观察上面各式,按此规律若
成立,观察上面各式,按此规律若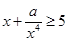 ,则正数
,则正数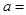 ( )
( )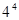
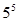
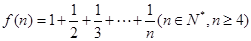 ,经计算得
,经计算得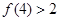 ,
,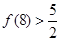 ,
,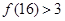 ,
,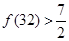
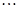 ,观察上述结果,可归纳出的一般结论为 .
,观察上述结果,可归纳出的一般结论为 .