题目内容
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.

(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求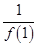 +
+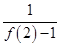 +
+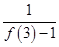 +…+
+…+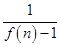 的值.
的值.

(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求
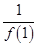 +
+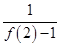 +
+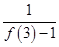 +…+
+…+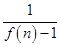 的值.
的值.(1)41
(2)f(n)=2n2-2n+1.
(3) -
- .
.
(2)f(n)=2n2-2n+1.
(3)
 -
- .
.解:(1)f(5)=41.
(2)因为f(2)-f(1)=4=4×1,
f(3)-f(2)=8=4×2,
f(4)-f(3)=12=4×3,
f(5)-f(4)=16=4×4,
……
由上式规律得出f(n+1)-f(n)=4n,
∴f(n)=f(1)+4(n-1)+4(n-2)+4(n-3)+…+4=2n2-2n+1(n≥2).
又n=1满足上式,
所以f(n)=2n2-2n+1.
(3)当n≥2时,
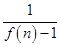 =
= =
= (
( -
- ),
),
∴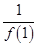 +
+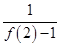 +
+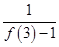 +…+
+…+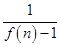
=1+ (1-
(1- +
+ -
- +
+ -
- +…+
+…+ -
- )
)
=1+ (1-
(1- )
)
= -
- .
.
(2)因为f(2)-f(1)=4=4×1,
f(3)-f(2)=8=4×2,
f(4)-f(3)=12=4×3,
f(5)-f(4)=16=4×4,
……
由上式规律得出f(n+1)-f(n)=4n,
∴f(n)=f(1)+4(n-1)+4(n-2)+4(n-3)+…+4=2n2-2n+1(n≥2).
又n=1满足上式,
所以f(n)=2n2-2n+1.
(3)当n≥2时,
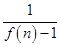 =
= =
= (
( -
- ),
),∴
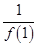 +
+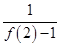 +
+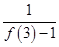 +…+
+…+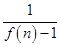
=1+
 (1-
(1- +
+ -
- +
+ -
- +…+
+…+ -
- )
)=1+
 (1-
(1- )
)=
 -
- .
.
练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 是一个自然数,
是一个自然数, 是
是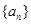 :
: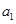 是自然数,
是自然数,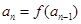 (
(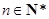 ,
,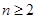 ).
).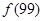 ,
,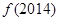 ;
;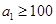 ,求证:
,求证: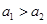 ;
;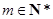 ,使得
,使得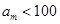 .
.
 ,则
,则 是函数
是函数 的极值点,因为
的极值点,因为 中,
中, 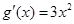 且
且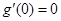 ,所以0是
,所以0是 是椭圆
是椭圆 :
: 且
且 为常数
为常数 上关于原点对称的两点,点
上关于原点对称的两点,点 是椭圆上的任意一点,若直线
是椭圆上的任意一点,若直线 和
和 的斜率都存在,并分别记为
的斜率都存在,并分别记为 ,
, ,那么
,那么 .类比双曲线
.类比双曲线 且
且 ,且下列三个关系:?
,且下列三个关系:? ?
? ?
? 有且只有一个正确,则
有且只有一个正确,则 .
. 的正方形,其中一个的某顶点在另一个的中心,则这两个正
的正方形,其中一个的某顶点在另一个的中心,则这两个正 ;类比到空间,有两个棱长均为
;类比到空间,有两个棱长均为
 的不等式
的不等式 的解集为(-1,2),解关于
的解集为(-1,2),解关于 ”,给出如下一种解法:
”,给出如下一种解法: 的解集为(-2,1),
的解集为(-2,1), 的不等式
的不等式 的解集为(-1,
的解集为(-1,  )
) (
(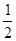 ,1),则关于
,1),则关于 的解集为________________
的解集为________________