题目内容
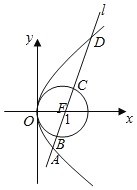
【题目】抛物线![]() 和圆
和圆![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 和圆
和圆![]() 分别交于四个点
分别交于四个点![]() (自下而上的顺序为
(自下而上的顺序为![]() ),则
),则![]() 的值为_________.
的值为_________.
【答案】16
【解析】
设![]() ,结合已知条件和抛物线的定义得|AF|=x1+2=|AB|+2,即|AB|=x1,同理可得:|CD|=x4,将直线的方程代入抛物线方程,利用韦达定理求得x1x4,即可得结果.
,结合已知条件和抛物线的定义得|AF|=x1+2=|AB|+2,即|AB|=x1,同理可得:|CD|=x4,将直线的方程代入抛物线方程,利用韦达定理求得x1x4,即可得结果.
设![]() ,∵y2=8x,焦点F(2,0),
,∵y2=8x,焦点F(2,0),![]() 的圆心为
的圆心为![]() ,半径
,半径![]() ,
,
所以直线![]() 既过抛物线
既过抛物线![]() 的焦点F,又过圆
的焦点F,又过圆![]() 的圆心.
的圆心.
抛物线的准线 l0:x=﹣2.由抛物线定义得:|AF|=x1+2,又∵|AF|=|AB|+2,∴|AB|=x1,同理:|CD|=x4,
则直线:y=x﹣2代入抛物线方程![]() ,得:x2﹣12x+4=0,∴x1x4=4,则|AB||CD|=4.又
,得:x2﹣12x+4=0,∴x1x4=4,则|AB||CD|=4.又![]() ,
,
综上所述,![]() =4
=4![]() 4=16
4=16
故答案为:16.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某生鲜批发店每天从蔬菜生产基地以5元/千克购进某种绿色蔬菜,售价8元/千克,若每天下午4点以前所购进的绿色蔬菜没有售完,则对未售出的绿色蔬菜降价处理,以3元/千克出售.根据经验,降价后能够把剩余蔬菜全部处理完毕,且当天不再进货.该生鲜批发店整理了过往30天(每天下午4点以前)这种绿色蔬菜的日销售量(单位:千克)得到如下统计数据(视频率为概率)(注:x,y∈N*)
每天下午4点前销售量 | 350 | 400 | 450 | 500 | 550 |
天数 | 3 | 9 | x | y | 2 |
(1)求在未来3天中,至少有1天下午4点前的销售量不少于450千克的概率.
(2)若该生鲜批发店以当天利润期望值为决策依据,当购进450千克比购进500千克的利润期望值大时,求x的取值范围.