题目内容
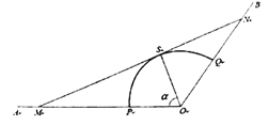
【题目】如图,射线![]() 和
和![]() 均为笔直的公路,扇形
均为笔直的公路,扇形![]() 区域(含边界)是一蔬菜种植园,其中
区域(含边界)是一蔬菜种植园,其中![]() 、
、![]() 分别在射线
分别在射线![]() 和
和![]() 上.经测量得,扇形
上.经测量得,扇形![]() 的圆心角(即
的圆心角(即![]() )为
)为![]() 、半径为1千米.为了方便菜农经营,打算在扇形
、半径为1千米.为了方便菜农经营,打算在扇形![]() 区域外修建一条公路
区域外修建一条公路![]() ,分别与射线
,分别与射线![]() 、
、![]() 交于
交于![]() 、
、![]() 两点,并要求
两点,并要求![]() 与扇形弧
与扇形弧![]() 相切于点
相切于点![]() .设
.设![]() (单位:弧度),假设所有公路的宽度均忽略不计.
(单位:弧度),假设所有公路的宽度均忽略不计.
(1)试将公路![]() 的长度表示为
的长度表示为![]() 的函数,并写出
的函数,并写出![]() 的取值范围;
的取值范围;
(2)试确定![]() 的值,使得公路
的值,使得公路![]() 的长度最小,并求出其最小值.
的长度最小,并求出其最小值.
【答案】⑴![]() ,其中
,其中![]() ,⑵当
,⑵当![]() 时,
时,![]() 长度的最小值为
长度的最小值为![]() 千米..
千米..
【解析】试题分析:
⑴由切线的性质可得OS⊥MN.则SM=![]() ,SN=
,SN=![]() , 据此可得
, 据此可得![]() ,其中
,其中![]() .
.
⑵ 利用换元法,令![]() ,则
,则![]() , 由均值不等式的结论有:
, 由均值不等式的结论有:![]() ,当且仅当
,当且仅当![]() 即
即![]() 时等号成立,即
时等号成立,即![]() 长度的最小值为
长度的最小值为![]() 千米.
千米.
试题解析:
⑴因为MN与扇形弧PQ相切于点S,所以OS⊥MN.
在![]() OSM中,因为OS=1,∠MOS=
OSM中,因为OS=1,∠MOS=![]() ,所以SM=
,所以SM=![]() ,
,
在![]() OSN中,∠NOS=
OSN中,∠NOS=![]() ,所以SN=
,所以SN=![]() ,
,
所以![]() ,
,
其中![]() .
.
⑵ 因为![]() ,所以
,所以![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() ,
,
由基本不等式得![]() ,
,
当且仅当![]() 即
即![]() 时取“=”.
时取“=”.
此时![]() ,由于
,由于![]() ,故
,故![]() .
.
答:⑴![]() ,其中
,其中![]() .
.
⑵当![]() 时,
时,![]() 长度的最小值为
长度的最小值为![]() 千米.
千米.

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案【题目】某快餐代卖店代售多种类型的快餐,深受广大消费者喜爱.其中,![]() 种类型的快餐每份进价为
种类型的快餐每份进价为![]() 元,并以每份
元,并以每份![]() 元的价格销售.如果当天20:00之前卖不完,剩余的该种快餐每份以
元的价格销售.如果当天20:00之前卖不完,剩余的该种快餐每份以![]() 元的价格作特价处理,且全部售完.
元的价格作特价处理,且全部售完.
(1)若该代卖店每天定制![]() 份
份![]() 种类型快餐,求
种类型快餐,求![]() 种类型快餐当天的利润
种类型快餐当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:份,
(单位:份,![]() )的函数解析式;
)的函数解析式;
(2)该代卖店记录了一个月![]() 天的
天的![]() 种类型快餐日需求量(每天20:00之前销售数量)
种类型快餐日需求量(每天20:00之前销售数量)
日需求量 |
|
|
|
|
|
|
天数 |
|
|
|
|
|
|
(i)假设代卖店在这一个月内每天定制![]() 份
份![]() 种类型快餐,求这一个月
种类型快餐,求这一个月![]() 种类型快餐的日利润(单位:元)的平均数(精确到
种类型快餐的日利润(单位:元)的平均数(精确到![]() );
);
(ii)若代卖店每天定制![]() 份
份![]() 种类型快餐,以
种类型快餐,以![]() 天记录的日需求量的频率作为日需求量发生的概率,求
天记录的日需求量的频率作为日需求量发生的概率,求![]() 种类型快餐当天的利润不少于
种类型快餐当天的利润不少于![]() 元的概率.
元的概率.
【题目】某地一商场记录了![]() 月份某
月份某![]() 天当中某商品的销售量
天当中某商品的销售量![]() (单位:
(单位:![]() )与该地当日最高气温
)与该地当日最高气温![]() (单位:
(单位:![]() )的相关数据,如下表:
)的相关数据,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)试求![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地
之间是正相关还是负相关;若该地![]() 月某日的最高气温是
月某日的最高气温是![]() ,试用所求回归方程预测这天该商品的销售量;
,试用所求回归方程预测这天该商品的销售量;
(3)假定该地![]() 月份的日最高气温
月份的日最高气温![]() ,其中
,其中![]() 近似取样本平均数
近似取样本平均数![]() ,
,![]() 近似取样本方差
近似取样本方差![]() ,试求
,试求![]() .
.
附:参考公式和有关数据 ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() ,且
,且![]() .
.