题目内容
设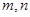 是两条不同的直线,
是两条不同的直线,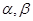 是两个不同的平面,则下列命题中的假命题是
是两个不同的平面,则下列命题中的假命题是
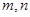 是两条不同的直线,
是两条不同的直线,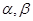 是两个不同的平面,则下列命题中的假命题是
是两个不同的平面,则下列命题中的假命题是A.若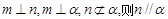 | B.若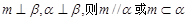 |
C.若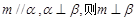 | D.若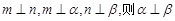 |
C
解:利用线面平行,面面垂直的判定定理和性质定理,我们可以判定得到结论。选项A,n与平面的关系平行。选项B中,也是满足的,选项C中,不成立。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
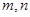 是两条不同的直线,
是两条不同的直线,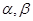 是两个不同的平面,则下列命题中的假命题是
是两个不同的平面,则下列命题中的假命题是A.若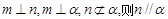 | B.若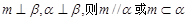 |
C.若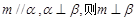 | D.若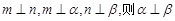 |

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案