题目内容
(本小题满分14分)
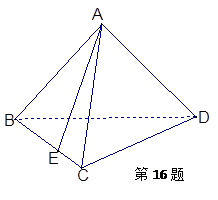
如图5所示,在三棱锥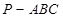 中,
中,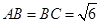 ,平面
,平面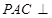 平面
平面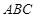 ,
,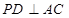 于点
于点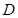 ,
, 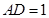 ,
,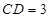 ,
,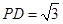 .
.
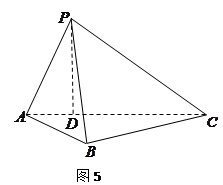
(1)证明△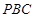 为直角三角形;
为直角三角形;
(2)求直线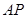 与平面
与平面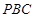 所成角的正弦值
所成角的正弦值
如图5所示,在三棱锥
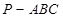 中,
中,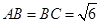 ,平面
,平面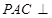 平面
平面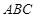 ,
,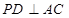 于点
于点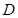 ,
, 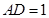 ,
,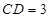 ,
,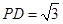 .
.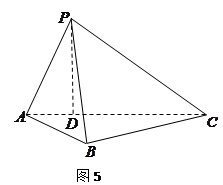
(1)证明△
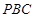 为直角三角形;
为直角三角形;(2)求直线
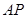 与平面
与平面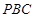 所成角的正弦值
所成角的正弦值(1)证明1:因为平面
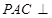 平面
平面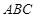 ,平面
,平面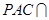 平面
平面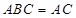 ,
, 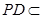 平面
平面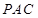 ,
,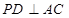 ,
,所以
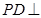 平面
平面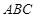 .
. 记
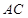 边上的中点为
边上的中点为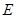 ,在△
,在△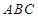 中,
中,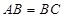 ,所以
,所以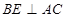 .
.因为
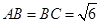 ,
,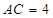 ,所以
,所以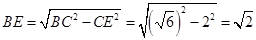 .
. 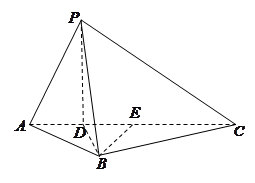
因为
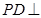
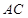 ,所以△
,所以△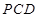 为直角三角形.
为直角三角形.因为
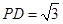 ,
,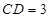 ,
,所以
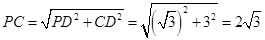 .
. 连接
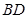 ,在
,在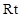 △
△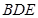 中,因为
中,因为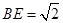 ,
,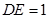 ,
,所以
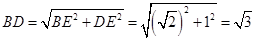 .
. 因为
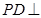 平面
平面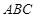 ,
,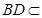 平面
平面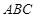 ,所以
,所以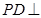
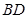 .
.在
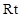 △
△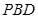 中,因为
中,因为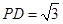 ,
,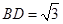 ,
,所以
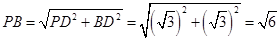 .
. 在
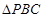 中,因为
中,因为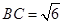 ,
,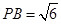 ,
,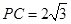 ,
,所以
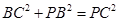 .
.所以
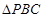 为直角三角形.
为直角三角形. 证明2:因为平面
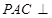 平面
平面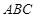 ,平面
,平面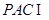 平面
平面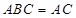 ,
, 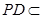 平面
平面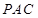 ,
,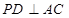 ,
,所以
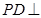 平面
平面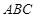 .
. 记
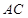 边上的中点为
边上的中点为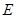 ,在△
,在△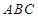 中,因为
中,因为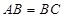 ,所以
,所以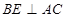 .
. 因为
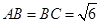 ,
,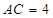 ,所以
,所以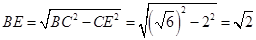 .
. 连接
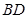 ,在
,在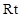 △
△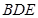 中,因为
中,因为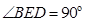 ,
,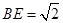 ,
,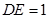 ,
,所以
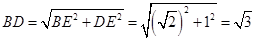 .
. 在△
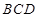 中,因为
中,因为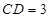 ,
,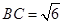 ,
,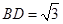 ,
,所以
 ,所以
,所以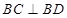 .
. 因为
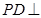 平面
平面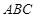 ,
,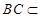 平面
平面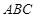 ,
,所以
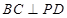 .
. 因为
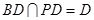 ,所以
,所以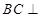 平面
平面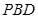 .
.因为
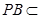 平面
平面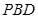 ,所以
,所以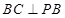 .
.所以
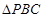 为直角三角形.
为直角三角形. (2)解法1:过点
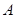 作平面
作平面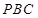 的垂线,垂足为
的垂线,垂足为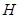 ,连
,连 ,
,则
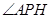 为直线
为直线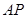 与平面
与平面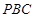 所成的角.
所成的角. 由(1)知,△
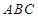 的面积
的面积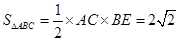 .
. 因为
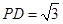 ,所以
,所以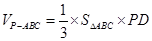
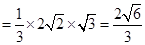 .
. 由(1)知
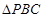 为直角三角形,
为直角三角形,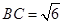 ,
,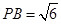 ,
,所以△
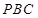 的面积
的面积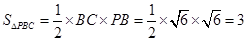 .
. 因为三棱锥
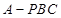 与三棱锥
与三棱锥 的体积相等,即
的体积相等,即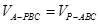 ,
,即
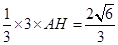 ,所以
,所以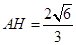 .
. 在
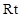 △
△ 中,因为
中,因为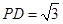 ,
,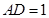 ,
,所以
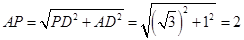 .
. 因为
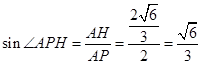 .
.所以直线
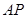 与平面
与平面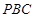 所成角的正弦值为
所成角的正弦值为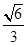 .
. 解法2:过点
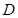 作
作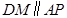 ,设
,设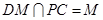 ,
,
则
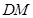 与平面
与平面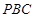 所成的角等于
所成的角等于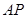 与平面
与平面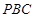 所成的角.
所成的角. 由(1)知
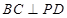 ,
,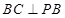 ,且
,且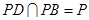 ,
,所以
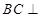 平面
平面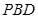 .
.因为
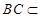 平面
平面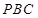 ,
,所以平面
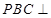 平面
平面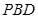 .
.过点
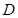 作
作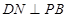 于点
于点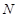 ,连接
,连接 ,
,则
 平面
平面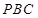 .
.所以
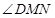 为直线
为直线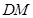 与平面
与平面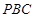 所成的角.
所成的角. 在
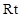 △
△ 中,因为
中,因为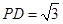 ,
,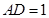 ,
,所以
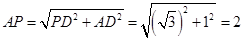 .
. 因为
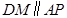 ,所以
,所以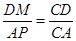 ,即
,即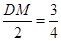 ,所以
,所以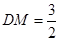 .
. 由(1)知
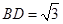 ,
,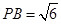 ,且
,且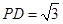 ,
,所以
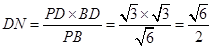 .
. 因为
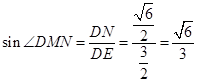 ,
,所以直线
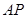 与平面
与平面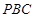 所成角的正弦值为
所成角的正弦值为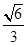 .
. 解法3:延长
 至点
至点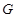 ,使得
,使得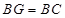 ,连接
,连接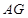 、
、 ,
, 在△
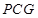 中,
中,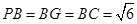 ,
,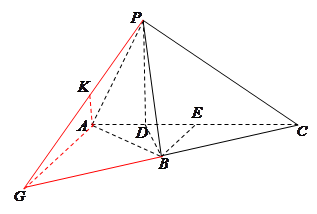
所以
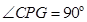 ,即
,即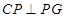 .
.在△
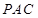 中,因为
中,因为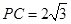 ,
,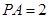 ,
,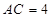 ,
,所以
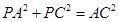 ,
,所以
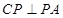 .
.因为
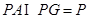 ,
,所以
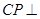 平面
平面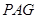 .
. 过点
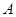 作
作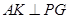 于点
于点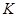 ,
,因为
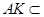 平面
平面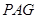 ,
,所以
 .
.因为
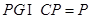 ,
,所以
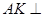 平面
平面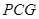 .
.所以
 为直线
为直线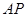 与平面
与平面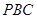 所成的角.
所成的角. 由(1)知,
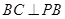 ,
,所以
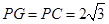 .
.在△
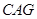 中,点
中,点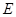 、
、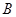 分别为边
分别为边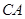 、
、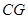 的中点,
的中点,所以
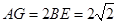 .
. 在△
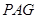 中,
中,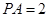 ,
,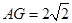 ,
,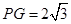 ,
,所以
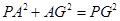 ,即
,即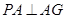 .
. 因为
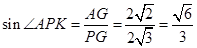 .
.所以直线
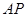 与平面
与平面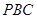 所成角的正弦值为
所成角的正弦值为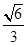 .
. 解法4:以点
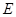 为坐标原点,以
为坐标原点,以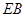 ,
,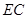 所在的直线分别为
所在的直线分别为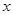 轴,
轴,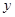 轴建立如图的空间直角坐标系
轴建立如图的空间直角坐标系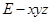 ,
, 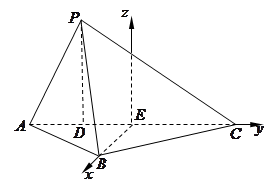
则
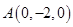 ,
, ,
,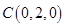 ,
,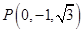 .
.于是
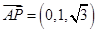 ,
,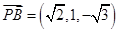 ,
,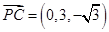 .
.设平面
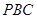 的法向量为
的法向量为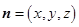 ,
,则
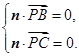
即
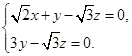
取
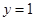 ,则
,则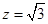 ,
,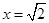 .
.所以平面
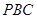 的一个法向量为
的一个法向量为 .
. 设直线
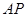 与平面
与平面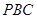 所成的角为
所成的角为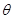 ,
,则
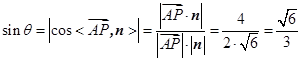 .
.所以直线
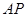 与平面
与平面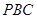 所成角的正弦值为
所成角的正弦值为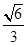 .
. 若第(1)、(2)问都用向量法求解,给分如下:
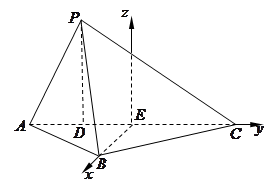
(1)以点
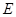 为坐标原点,以
为坐标原点,以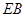 ,
,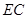 所在的直线分别为
所在的直线分别为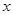 轴,
轴,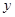 轴建立如图的空间直角坐标系
轴建立如图的空间直角坐标系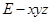 ,
, 则
 ,
,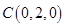 ,
,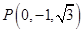 .
.于是
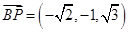 ,
,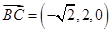 .
.因为
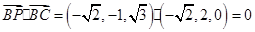 ,
,所以
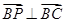 .
.所以
 .
.所以
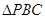 为直角三角形.
为直角三角形. (2)由(1)可得,
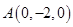 .
.于是
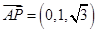 ,
,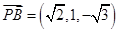 ,
,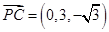 .
.设平面
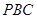 的法向量为
的法向量为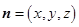 ,
,则
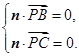 即
即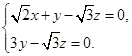
取
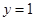 ,则
,则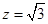 ,
,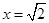 .
.所以平面
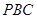 的一个法向量为
的一个法向量为 .
. 设直线
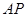 与平面
与平面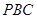 所成的角为
所成的角为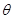 ,
,则
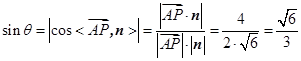 .
.所以直线
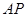 与平面
与平面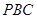 所成角的正弦值为
所成角的正弦值为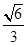 .
. 略

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
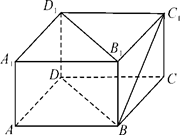
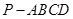 的底面
的底面 为矩形,且
为矩形,且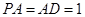 ,
,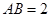 ,
,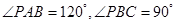 ,(Ⅰ)平面
,(Ⅰ)平面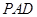 与平面
与平面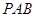 是否垂直?并说明理由;(Ⅱ)求直线
是否垂直?并说明理由;(Ⅱ)求直线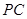 与平面
与平面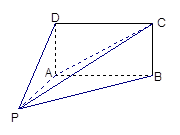
 中,点
中,点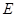 是
是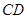 的中点.
的中点. 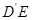 与
与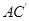 所成的角的余弦值;
所成的角的余弦值;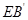 与平面
与平面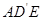 所成的角的余弦值.
所成的角的余弦值.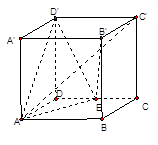
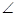 BAD=
BAD=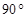 ,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.
,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.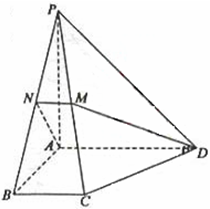
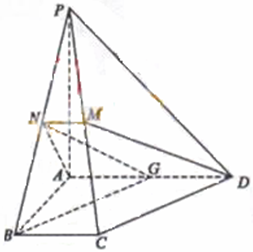
 矩形ABCD所在平面,PA=AD=
矩形ABCD所在平面,PA=AD=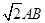 ,E为线段PD上一点,G为线段PC的中点.
,E为线段PD上一点,G为线段PC的中点.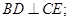
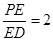 时,求证:BG//平面AEC.
时,求证:BG//平面AEC.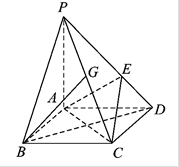
 中,二面角
中,二面角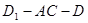 的正切值为
的正切值为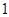
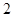
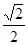
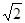 .
.