题目内容
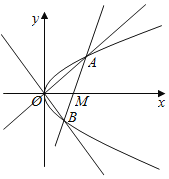
【题目】已知抛物线C：y2＝4x，直线l交于A，B两点，O为坐标原点，直线OA，OB的斜率分别为k1，k2，若k1k2＝﹣2，则△AOB面积的最小值为_____．
【答案】4
【解析】
由题意可设直线AB的方程为： x＝my+b与抛物线方程联立可得根与系数的关系、利用斜率公式得出直线AB过定点，再利用三角形的面积计算公式即可得出结论.
由题意可设直线AB的方程为：x＝my+b．
联立
，化为y2﹣4my﹣4b＝0，
∴y1+y2＝4m，y1y2＝﹣4b．
∵直线OA，OB的斜率分别为k1，k2，k1k2＝﹣2．
∴
2．
∴y1y2＝﹣8，
∴﹣4b＝﹣8，
∴b＝2．
因此直线AB过定点M（2，0）．
∴△AOB面积S
|y1﹣y2|
，
因此当m＝0时，△AOB的面积取得最小值4
．
故答案为：
.
练习册系列答案
相关题目
