Question

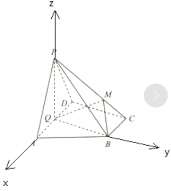
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC＝90°，平面PAD⊥底面ABCD，Q为AD的中点，PA＝PD＝AD＝2，BC＝1，.

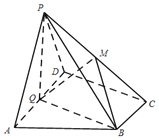
（1）求证：平面PQB⊥平面PAD；

（2）若M是棱PC上的一点，且满足，求二面角M﹣BQ﹣C的大小.

Answer 1

【答案】（1）证明见解析；

（2）

【解析】

（1）推导出四边形BCDQ是平行四边形，从而，进而平面PQB，由此能证明平面PQB⊥平面PAD.

（2）以Q为原点，QA为x轴，QB为y轴，QP为z轴建立空间直角坐标系，求出平面MBQ，BQC的法向量，利用向量法求出二面角M﹣BQ﹣C的大小.

（1）为AD中点，PA＝PD＝AD＝2，BC＝1

故四边形BCDQ是平行四边形

又底面ABCD为直角梯形，AD∥BC，∠ADC＝90°

，又

平面PQB

平面PAD

平面PQB⊥平面PAD.

（2）平面PQB⊥平面PAD，平面PQB 平面PAD=PQ

PQ⊥平面PAD

以Q为原点，QA为x轴，QB为y轴，QP为z轴建立空间直角坐标系

则

设，即

设平面MAB的法向量为：

则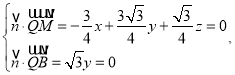：取

则

平面BQC的法向量为

设二面角M﹣BQ﹣C的平面角为，

则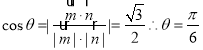

故二面角M﹣BQ﹣C的平面角为.