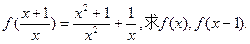题目内容
已知α,β是方程4x2-4tx-1=0(t∈R)的两个实数根,函数f(x)=的定义域为[α,β].
(1)判断f(x)在[α,β]上的单调性,并证明你的结论;
(2)设g(t)=maxf(x)-minf(x),求函数g(t)的最小值
(1)f(x)在[α,β]上为增函数
∵f(x)=,∴f′(x)=,
∵当x∈(α,β)时,4x2-4tx-1<0,
∴当x∈(α,β)时,-2x2+2tx+>0,
∴当x∈(α,β)时,-2x2+2tx+2>0,
∴f′(x)>0,∴f(x)在[α,β]上单增.
(2)由题意及(1)可知,f(x)max=f(β),f(x)min=f(α),
∴g(t)=f(β)-f(α)=-
=
∵α+β=t,αβ=-,∴β-α==,
α2+β2=(α+β)2-2αβ=t2+,
∴g(t)=,t∈R,
令=U,则t2=U2-1,U∈[1,+∞),
∴g(t)==,
∵′=>0,
∴在[1,+∞)单调递增,
∴当U=1,t=0时,g(t)min=.
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
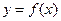 在定义域
在定义域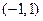 上是减函数,满足f(1-a)+f(1-
上是减函数,满足f(1-a)+f(1- 2a)〈0,求
2a)〈0,求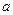 的取值范围。
的取值范围。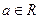 ,
,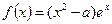
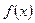 的单调区间
的单调区间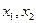 是
是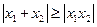 ,若
,若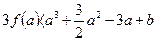 恒成立,求实数b的取值范围
恒成立,求实数b的取值范围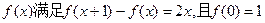
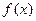 的解析式;
的解析式;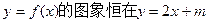 的图象上方,求实数m的范围.
的图象上方,求实数m的范围. 在
在 上为增函数.
上为增函数. ,若
,若 能表示成一个奇函数
能表示成一个奇函数 和一个偶函数
和一个偶函数 的和.
的和. 上都是减函数,求
上都是减函数,求 的取值范围.
的取值范围.
 )已知
)已知