题目内容
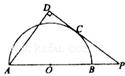
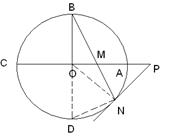
如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,点 是线段
是线段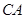 延长线上一点,连接PN,且满足
延长线上一点,连接PN,且满足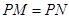
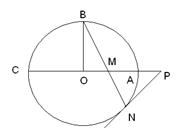
(Ⅰ)求证: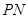 是圆O的切线;
是圆O的切线;
(Ⅱ)若圆O的半径为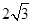 ,OA=
,OA=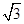 OM,求MN的长.
OM,求MN的长.
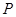 是线段
是线段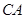 延长线上一点,连接PN,且满足
延长线上一点,连接PN,且满足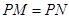

(Ⅰ)求证:
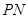 是圆O的切线;
是圆O的切线;(Ⅱ)若圆O的半径为
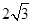 ,OA=
,OA=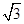 OM,求MN的长.
OM,求MN的长. (Ⅰ)见解析(Ⅱ) 2
(Ⅰ)证明:如图,连接ON,∵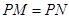 ,则
,则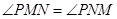 , 2分
, 2分
又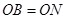 ,则
,则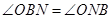 .
.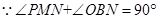 ,∴
,∴
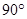 , 4分
, 4分
∴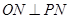 ,故
,故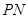 是圆O的切线; 5分
是圆O的切线; 5分
(Ⅱ)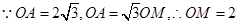 .在
.在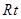 △BOM中,
△BOM中,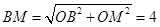 ,,延长BO交圆O于点D,连接DN,由条件知△BOM∽△BND,于是
,,延长BO交圆O于点D,连接DN,由条件知△BOM∽△BND,于是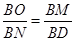 ,
,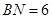 ,即MN=BN-BM=6-4=2. 10分
,即MN=BN-BM=6-4=2. 10分
【命题意图】本题考察切线的判定定理、三角形相似等基础知识,意在考察学生推理证明和逻辑思维能力.
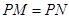 ,则
,则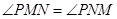 , 2分
, 2分又
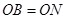 ,则
,则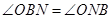 .
.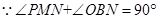 ,∴
,∴
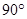 , 4分
, 4分∴
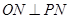 ,故
,故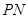 是圆O的切线; 5分
是圆O的切线; 5分(Ⅱ)
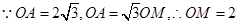 .在
.在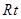 △BOM中,
△BOM中,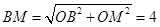 ,,延长BO交圆O于点D,连接DN,由条件知△BOM∽△BND,于是
,,延长BO交圆O于点D,连接DN,由条件知△BOM∽△BND,于是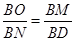 ,
,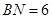 ,即MN=BN-BM=6-4=2. 10分
,即MN=BN-BM=6-4=2. 10分
【命题意图】本题考察切线的判定定理、三角形相似等基础知识,意在考察学生推理证明和逻辑思维能力.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 ,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.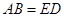 .
.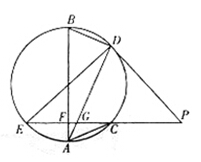
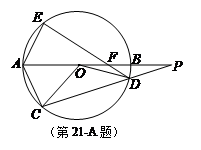
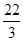 ,PO=12,则⊙O的半径是________.
,PO=12,则⊙O的半径是________.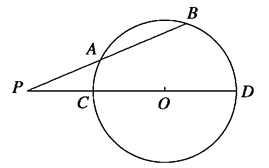
 是圆
是圆 的切线,切点为
的切线,切点为 ,
, 交圆
交圆 、
、 两点,且
两点,且 ,
,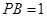 ,则
,则 的长为 .
的长为 .
 PD.若PC=4, PB=2,则CD=____________.
PD.若PC=4, PB=2,则CD=____________.