题目内容
如图,已知PA与⊙O相切,A为切点,PBC为割线,D为⊙O上一点,AD、BC相交于点E.
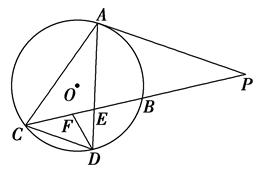
(1)若AD=AC,求证:AP∥CD;
(2)若F为CE上一点使得∠EDF=∠P,已知EF=1,EB=2,PB=4,求PA的长.

(1)若AD=AC,求证:AP∥CD;
(2)若F为CE上一点使得∠EDF=∠P,已知EF=1,EB=2,PB=4,求PA的长.
(1)若AD=AC,AP∥CD;(2) PA=6.
(1)∵PA是⊙O的切线,AD是弦,
∴∠PAD=∠ACD.
∵AD=AC,∴∠ADC=∠ACD,
∴∠PAD=∠ADC,
∴AP∥CD.
(2)∵∠EDF=∠P,又∠DEF=∠PEA,
∴△DEF △PEA,有
△PEA,有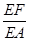 =
=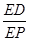 ,
,
即EF·EP=EA·ED.而AD、BC是⊙O的相交弦,
∴EC·EB=EA·ED,
故EC·EB=EF·EP,
∴EC=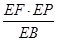 =
=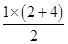 =3.
=3.
由切割线定理有PA2=PB·PC=4×(3+2+4)=36,
∴PA=6.
∴∠PAD=∠ACD.
∵AD=AC,∴∠ADC=∠ACD,
∴∠PAD=∠ADC,
∴AP∥CD.
(2)∵∠EDF=∠P,又∠DEF=∠PEA,
∴△DEF
 △PEA,有
△PEA,有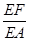 =
=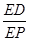 ,
,即EF·EP=EA·ED.而AD、BC是⊙O的相交弦,
∴EC·EB=EA·ED,
故EC·EB=EF·EP,
∴EC=
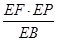 =
=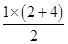 =3.
=3.由切割线定理有PA2=PB·PC=4×(3+2+4)=36,
∴PA=6.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
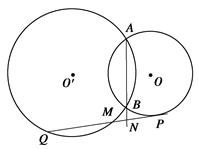
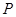 是线段
是线段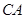 延长线上一点,连接PN,且满足
延长线上一点,连接PN,且满足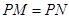
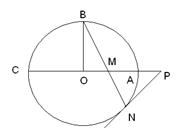
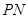 是圆O的切线;
是圆O的切线;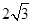 ,OA=
,OA=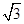 OM,求MN的长.
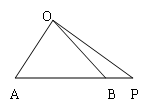
OM,求MN的长. 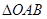 是等腰三角形,
是等腰三角形,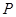 是底边
是底边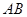 延长线上一点,
延长线上一点,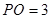 ,
,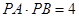 ,则腰长
,则腰长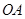 = .
= .
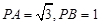 ,则
,则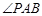 =_________.
=_________.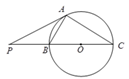
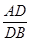 =2,那么△ADE与四边形DBCE的面积比是( )
=2,那么△ADE与四边形DBCE的面积比是( )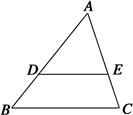
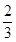 B.
B.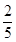 C.
C.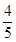 D.
D.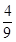
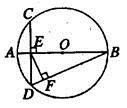
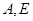 是半圆周上的两个三等分点,直径
是半圆周上的两个三等分点,直径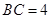 ,
,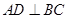 ,垂足为D,
,垂足为D, 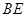 与
与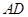 相交与点F,则
相交与点F,则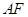 的长为 。
的长为 。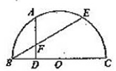
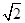 ,求AF的长.
,求AF的长.