题目内容
3.在棱长都相等的四面体ABCD中,E、F分别是CD、BC的中点,则异面直线AE、DF所成角的余弦值是$\frac{1}{6}$.分析 画出四面体ABCD,并设BC=4,取CF的中点为M,则∠AEM或其补角便是异面直线AE、DF所成角,这时候可以求出CM,CE,ME,而由余弦定理可以求出AM,从而在△AEM中由余弦定理即可求出cos∠AEM,这便得到异面直线AE、DF所成角的余弦值.
解答 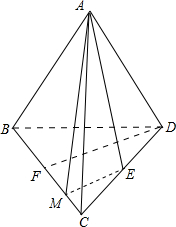 解:如图,
解:如图,
设BC=4,取CF中点M,连接AM,ME;
∵E是CD中点;
∴ME∥DF;
∴∠AEM或其补角便是异面直线AE,DF所成角;
则:$DF=2\sqrt{3}$,$ME=\sqrt{3}$,$AE=2\sqrt{3}$,CE=2,CM=1;
∴在△ACM中,由余弦定理得:AM2=CA2+CM2-2CA•CM•cos60°=16+1-4=13;
∴在△AME中,由余弦定理得:cos∠AEM=$\frac{M{E}^{2}+A{E}^{2}-A{M}^{2}}{2ME•AE}=\frac{3+12-13}{2\sqrt{3}•2\sqrt{3}}=\frac{1}{6}$;
∴异面直线AE、DF所成角的余弦值是$\frac{1}{6}$.
故答案为:$\frac{1}{6}$.
点评 考查异面直线所成角的概念及其求法,清楚异面直线所成角的范围,等边三角形的中线也是高线,直角三角形边角的关系,以及余弦定理的应用.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
11.函数y=ex+x-2的零点个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
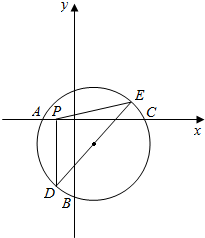 如图,直角三角形ABC的顶点坐标A(-2,0)、B(0,$-2\sqrt{2}$),顶点C在x轴上,点P为线段OA的中点,设圆M是△ABC的外接圆,若DE是圆M的任意一条直径,试探究$\overrightarrow{PD}•\overrightarrow{PE}$是否是定值?若是,求出定值;若不是,请说明理由.
如图,直角三角形ABC的顶点坐标A(-2,0)、B(0,$-2\sqrt{2}$),顶点C在x轴上,点P为线段OA的中点,设圆M是△ABC的外接圆,若DE是圆M的任意一条直径,试探究$\overrightarrow{PD}•\overrightarrow{PE}$是否是定值?若是,求出定值;若不是,请说明理由.