题目内容
14.设x=3是函数f(x)=(x2+ax+b)e3-x,(x∈R)的一个极值点.(1)求a与b的关系式(用a表示b),并求f(x)的单调区间;
(2)设$a>0,g(x)=\frac{{{e^2}{f^'}(x)}}{3-x}$,若存在ξ1,ξ2∈[0,4],使得$|{f({ξ_1})-g({ξ_2})}|<5{e^2}-6$成立,求a的取值范围.
分析 (1)由已知中函数f(x)=(x2+ax+b)e3-x(x∈R)的一个极值点是x=3.我们根据函数在某点取得极值的条件,易得f′(3)=0,进而构造方程求出a与b的关系式,分析函数在各个区间上的符号,即可得到答案.
(2)根据g(x)的表达式,利用导数法确定函数的单调性,再根据(1)的结论,我们可以构造一个关于a的不等式,解不等式即可得到答案.
解答 解:(1)f′(x)=-e3-x,(1分)
由f′(3)=0,得-e3-3=0,即得b=-3-2a,(2分)
则f′(x)=-(x-3)(x+a+1)e3-x.
令f′(x)=0,得x1=3或x2=-a-1,由于x=3是极值点,∴-a-1≠3,即a≠-4,(4分)
当a<-4时,x2>3=x1,则在区间(-∞,3)上,f′(x)<0,
f(x)为减函数;在区间(3,-a-1)上,f′(x)>0,f(x)为增函数;
在区间(-a-1,+∞)上,f′(x)<0,f(x)为减函数. (5分)
当a>-4时,x2<3=x1,则在区间(-∞,-a-1)上,f′(x)<0,f(x)为减函数;
在区间(-a-1,3)上,f′(x)>0,f(x)为增函数;在区间(3,+∞)上,f′(x)<0,f(x)为减函数;
(2)由(Ⅰ)知,当a>0时,f(x)在区间(0,3)上的单调递增,在区间(3,4)上单调递减,
由于f(x)连续,而f(0)=-(2a+3)e3<0,f(4)=(2a+13)e-1>0,f(3)=a+6,
那么f(x)在区间上的值域是:[-(2a+3)e3,a+6],
又g(x)=$\frac{{-e}^{2}(x-3)(x+a+1{)e}^{3-x}}{3-x}$=(x+a+1)e5-x,(a>0,x∈[0,4]),
g′(x)=-e5-x(x+a)<0,
∴g(x)在区间上是减函数,而g(0)=(a+1)e5,g(4)=(a+5)e,
∴它在区间上的值域是:[e(a+5),e5(a+1)],
∴只需e(a+5)-(a+6)<5e2-6即可,解得:a<5e,
∴a的范围是:(0,5e).
点评 本题考查的知识点是函数在某点取得极值的条件,利用导数研究函数的单调性,其中根据已知中的函数的解析式,结合导数公式,求出函数的导函数的解析式,是解答本题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| A. | 2+i | B. | 2 i | C. | 1+i | D. | -1-i |
| A. | 夹在两个平行平面间的平行线段相等 | |
| B. | 过直线l外一点M有且仅有一个平面α与直线l垂直 | |
| C. | 垂直于同一条直线的两个平面平行 | |
| D. | 空间中如果两个角的两边分别对应平行,那么这两个角相等 |
 如图所示,圆O的直径AB=10,C为圆周上一点,BC=5,过C作圆的切线l,则点A到直线l的距离AD为$\frac{15}{2}$.
如图所示,圆O的直径AB=10,C为圆周上一点,BC=5,过C作圆的切线l,则点A到直线l的距离AD为$\frac{15}{2}$.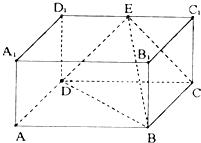 在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连结ED,EC,EB和DB.
在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连结ED,EC,EB和DB.