题目内容
【题目】如图，在平面直角坐标系xOy中，设点M（x0 ， y0）是椭圆C： 
+y2=1上一点，从原点O向圆M：（x﹣x0）2+（y﹣y0）2=r2作两条切线分别与椭圆C交于点P，Q．直线OP，OQ的斜率分别记为k1 ， k2
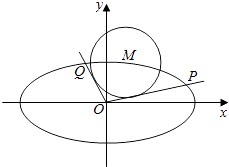
（1）若圆M与x轴相切于椭圆C的右焦点，求圆M的方程；
（2）若r= 
，①求证：k1k2=﹣ 
；②求OPOQ的最大值．
【答案】
（1）解：椭圆C的右焦点是（ 
，0），x= ，代入 
+y2=1，可得y=± 
，
∴圆M的方程：（x﹣ ）2+（y 
）2= 
；
（2）解：因为直线OP：y=k1x，OQ：y=k2x，与圆R相切，
所以直线OP：y=k1x与圆M：（x﹣x0）2+（y﹣y0）2= 
联立，可得（1+k12）x2﹣（2x0+2k1y0）x+x02+y02﹣ =0
同理（1+k22）x2﹣（2x0+2k2y0）x+x02+y02﹣ =0，
由判别式为0，可得k1，k2是方程（x02﹣ ）k2﹣2x0y0k+y02﹣ =0的两个不相等的实数根，
∴k1k2=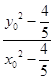 
，
因为点M（x0，y0）在椭圆C上，所以y2=1﹣ 
，
所以k1k2= =﹣ ；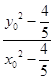
（i）当直线OP，OQ不落在坐标轴上时，设P（x1，y1），Q（x2，y2），
因为4k1k2+1=0，所以 
+1=0，即y12y22= 
x12x22，
因为P（x1，y1），Q（x2，y2）在椭圆C上，所以y12y22=（1﹣ 
）（1﹣ 
）= x12x22，
整理得x12+x22=4，
所以y12+y22=1
所以OP2+OQ2=5．
（ii）当直线落在坐标轴上时，显然有OP2+OQ2=5，
综上：OP2+OQ2=5
所以OPOQ≤ （OP2+OQ2）=2.5，
所以OPOQ的最大值为2.5．
【解析】（1）椭圆C的右焦点是（ 
，0），x= ，代入 
+y2=1，可得y=± 
，求出圆的圆心，然后求圆M的方程；（2）①因为直线OP：y=k1x，OQ：y=k2x，与圆R相切，推出k1，k2是方程（1+k2）x2﹣（2x0+2ky0）x+x02+y02﹣ 
=0的两个不相等的实数根，利用韦达定理推出k1k2．结合点M（x0，y0）在椭圆C上，证明k1k2=﹣ 
．②（i）当直线OP，OQ不落在坐标轴上时，设P（x1，y1），Q（x2，y2），通过4k1k2+1=0，推出y12y22= 
x12x22，利用P（x1，y1），Q（x2，y2），在椭圆C上，推出OP2+OQ2=5，即可求出OPOQ的最大值．
