题目内容
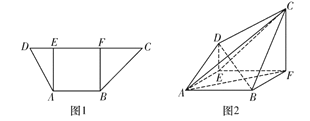
【题目】在梯形![]() 中(图1),
中(图1),![]() ,
,![]() ,
,![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() 、
、![]() ,且
,且![]() ,将梯形
,将梯形![]() 沿
沿![]() 、
、![]() 同侧折起,使得
同侧折起,使得![]() ,且
,且![]() ,得空间几何体
,得空间几何体![]() (图2).直线
(图2).直线![]() 与平面
与平面![]() 所成角的正切值是
所成角的正切值是![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求多面体![]() 的体积.
的体积.
【答案】(1)见证明;(2) ![]()
【解析】
(1)连接BE交AF于O,取AC的中点H,连接OH,可得OH∥CF,OH![]() ,再由已知DE∥CF,DE
,再由已知DE∥CF,DE![]() ,可得四边形OEDH为平行四边形,则DH∥OE.由线面平行的判定可得EO∥面ACD,即BE∥面ACD;(2)证明
,可得四边形OEDH为平行四边形,则DH∥OE.由线面平行的判定可得EO∥面ACD,即BE∥面ACD;(2)证明![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,利用
,利用![]() 求解即可
求解即可
(1)连接![]() 交
交![]() 于点
于点![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
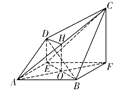
因为四边形![]() 为矩形,则
为矩形,则![]() 是
是![]() 的中位线,
的中位线,
所以![]() 且
且![]() ,
,
由已知得![]() 且
且![]() ,
,
所以![]() 且
且![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
即![]() 平面
平面![]() ;
;
(2)由已知![]() ,
,![]() ,
,![]() ,
,
可得![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
因为直线![]() 与平面
与平面![]() 所成角的正切值是
所成角的正切值是![]() ,
,
所以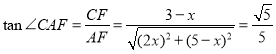 ,解得:
,解得:![]() ,
,
![]() ,
,![]() ,
,
![]() .
.

【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率( | 级数 | 全月应纳税所得额 | 税率( |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
… | … | … | … | … | … |
(1)假如小红某月的工资、薪金等所得税前收入总和不高于8000元,记![]() 表示总收入,
表示总收入,![]() 表示应纳的税,试写出调整前后
表示应纳的税,试写出调整前后![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入 (元) |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
(3)小红该月的工资、薪金等税前收入为7500元时,请你帮小红算一下调整后小红的实际收入比调整前增加了多少?
【题目】据史载知,新华网:北京2008年11月9日电,国务院总理温家宝主持召开国务院常务会议.研究部署进一步扩大内需促进经济平稳较快增长的措施,以应对日趋严峻的全球性世界经济金融危机,在提高城乡居民特别是低收入人群的收入水平政策措施的刺激下,某零售店当时近5个月的销售额和利润额数据统计如下表:
月份 | 2 | 3 | 4 | 5 | 6 |
销售额x/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额y/百万元 | 2 | 3 | 3 | 4 | 5 |
(1)若x与y之间是线性相关关系,求利润额y关于销售额x的线性回归方程![]() ;
;
(2)若9月份的销售额为8千万元,试利用(1)的结论估计该零售店9月份的利润额.
参考公式: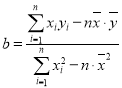 ,
,![]() .
.