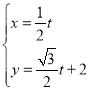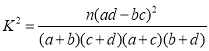题目内容
【题目】设函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)当![]() 时,判断函数
时,判断函数![]() 的单调性;
的单调性;
(2)若直线![]() 是函数
是函数![]() 的切线,求实数
的切线,求实数![]() 的值;
的值;
(3)当![]() 时,证明:
时,证明:![]() .
.
【答案】(1)![]() 在区间
在区间![]() 上单调递增.(2)
上单调递增.(2)![]() (3)见证明
(3)见证明
【解析】
(1)先由解析式,得到函数定义域,对函数求导,根据![]() ,即可得出结果;
,即可得出结果;
(2)先设切点为![]() ,根据切线方程为
,根据切线方程为![]() ,得到
,得到![]() ,再对函数求导,得到
,再对函数求导,得到![]() ,设
,设![]() ,用导数方法研究其单调性,得到最值,即可求出结果;
,用导数方法研究其单调性,得到最值,即可求出结果;
(3)先对函数求导,设![]() ,用导数方法研究
,用导数方法研究![]() 单调性,进而可判断出
单调性,进而可判断出![]() 单调性,即可得出结论成立.
单调性,即可得出结论成立.
解:(1)函数![]() 的定义域为
的定义域为![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() 在区间
在区间![]() 上单调递增.
上单调递增.
(2)设切点为![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,得
,得![]() ,
,
所以![]() .
.
设![]() ,则
,则![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
所以![]() .
.
因为方程![]() 仅有一解
仅有一解![]() ,
,
所以![]() .
.
(3)因为![]() ,
,
设![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 单调递增.
单调递增.
因为![]() ,
,![]() ,
,
所以存在![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递增,
单调递增,
所以![]() .
.
因为![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]()
![]() .
.

练习册系列答案
相关题目
【题目】已知某商品每件的生产成本![]() (元)与销售价格
(元)与销售价格![]() (元)具有线性相关关系,对应数据如表所示:
(元)具有线性相关关系,对应数据如表所示:
| 5 | 6 | 7 | 8 |
| 15 | 17 | 21 | 27 |
(1)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该商品的月销售量![]() (千件)与生产成本
(千件)与生产成本![]() (元)的关系为
(元)的关系为![]() ,
,![]() ,根据(1)中求出的线性回归方程,预测当
,根据(1)中求出的线性回归方程,预测当![]() 为何值时,该商品的月销售额最大.
为何值时,该商品的月销售额最大.
附: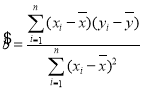 ,
,![]() .
.