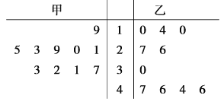
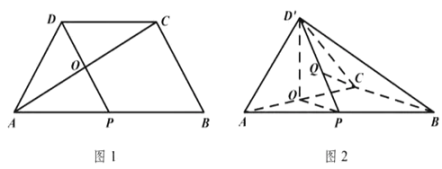题目内容
【题目】已知非空集合![]() 满足
满足![]() .若存在非负整数
.若存在非负整数![]() ,使得当
,使得当![]() 时,均有
时,均有![]() ,则称集合
,则称集合![]() 具有性质
具有性质![]() .记具有性质
.记具有性质![]() 的集合
的集合![]() 的个数为
的个数为![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的表达式.
的表达式.
【答案】(1)![]() (2)
(2)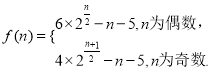
【解析】
试题(1)因为![]() ,所以
,所以![]() ,对应的
,对应的![]() 分别为
分别为![]() ,故
,故![]() .(2)通过研究相邻两项之间关系,得递推关系,进而可求通项:设当
.(2)通过研究相邻两项之间关系,得递推关系,进而可求通项:设当![]() 时,具有性质
时,具有性质![]() 的集合
的集合![]() 的个数为
的个数为![]() ,当
,当![]() 时,
时,![]() ,关键计算
,关键计算![]() 关于
关于![]() 的表达式,① 当
的表达式,① 当![]() 为偶数时,
为偶数时,![]() 为奇数,
为奇数,![]() ;② 当
;② 当![]() 为奇数时,
为奇数时,![]() 为偶数,
为偶数,![]() ,最后根据累加法解得
,最后根据累加法解得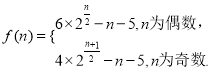
试题解析:(1)当![]() 时,
时,![]() 具有性质
具有性质![]() ,
,
对应的![]() 分别为
分别为![]() ,故
,故![]() .
.
(2)可知当![]() 时,具有性质
时,具有性质![]() 的集合
的集合![]() 的个数为
的个数为![]() ,
,
则当![]() 时,
时,![]() ,
,
其中![]() 表达
表达![]() 也具有性质
也具有性质![]() 的集合
的集合![]() 的个数,
的个数,
下面计算![]() 关于
关于![]() 的表达式,
的表达式,
此时应有![]() ,即
,即![]() ,故对
,故对![]() 分奇偶讨论,
分奇偶讨论,
① 当![]() 为偶数时,
为偶数时,![]() 为奇数,故应该有
为奇数,故应该有![]() ,
,
则对每一个![]() ,
,![]() 和
和![]() 必然属于集合
必然属于集合![]() ,且
,且![]() 和
和![]() ,…,
,…,
![]() 和
和![]() 共有
共有![]() 组数,每一组数中的两个数必然同时属于或不属于集合
组数,每一组数中的两个数必然同时属于或不属于集合![]() ,
,
故对每一个![]() ,对应的具有性质
,对应的具有性质![]() 的集合
的集合![]() 的个数为
的个数为
![]() ,
,
所以![]() ,
,
② 当![]() 为奇数时,
为奇数时,![]() 为偶数,故应该有
为偶数,故应该有![]() ,
,
同理![]() ,
,
综上,可得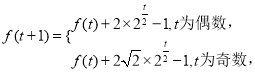 又
又![]() ,
,
由累加法解得
即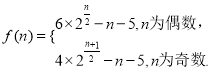

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目