Question

【题目】已知数列的前项和，数列的前项和，，则正整数的最大值为_________.

Answer 1

【答案】3

【解析】

运用数列的递推式，结合等比数列的定义、通项公式可得an，Sn，再由数列的分组求和，结合等比数列的求和公式，以及数列的单调性，解不等式可得所求最大值．

Sn＝2﹣1，可得＝S1＝2﹣1，解得＝1；

n≥2时，＝Sn﹣Sn﹣1＝2﹣1﹣2 +1，

则＝2，可得为首项为1，公比为2的等比数列，

可得＝2n﹣1，Sn＝2n﹣1，

Sn1＝2n﹣1+（）n﹣1+1＝2n+（）n﹣1，

Tn＝（2+4+…+2n）+（1（）n﹣1）

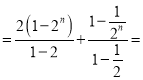2n+1﹣（）n﹣1，

可得Tn是一个增函数（增函数+增函数=增函数），随着n的增大而增大，T3，

由，可得n≤3，即n的最大值为3．

故答案为：3．