题目内容
设点P是曲线y=2x2上的一个动点,曲线y=2x2在点P处的切线为l,过点P且与直线l垂直的直线与曲线y=2x2的另一交点为Q,则PQ的最小值为_____________
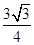
试题分析:设P的坐标为(a,
 ),由y‘=4x得l的斜率为4a,所以,直线PQ的斜率为=
),由y‘=4x得l的斜率为4a,所以,直线PQ的斜率为=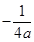 ,
,所以,PQ的方程为:y-
 =
=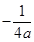 (x-a),
(x-a),与y=2x2联立,整理得,
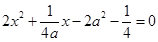 ,所以,由韦达定理,
,所以,由韦达定理,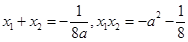 ,
,由弦长公式得,PQ=
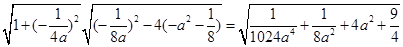 ,利用导数研究此函数的最值,知,PQ的最小值为
,利用导数研究此函数的最值,知,PQ的最小值为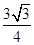 。
。点评:难题,本题综合性较强,考查知识覆盖面广,总体看解答思路比较明确,但计算繁琐,对学生能力要求较高。曲线切线的斜率,等于函数在切点的导函数值。

练习册系列答案
相关题目
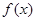 的导函数
的导函数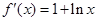 ,且
,且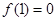 ,设
,设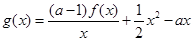 ,
,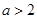 .
.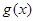 在区间
在区间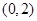 上的单调性;
上的单调性;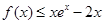 ;
;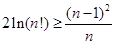 .
.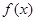 是定义在
是定义在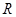 上的奇函数,
上的奇函数,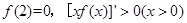 ,则不等式
,则不等式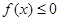 的解集是
的解集是 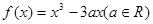
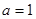 时,求
时,求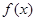 在
在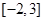 的最小值;
的最小值;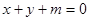 对任意的
对任意的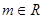 都不是曲线
都不是曲线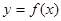 的切线,求
的切线,求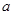 的取值范围;
的取值范围;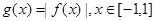 ,求
,求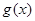 的最大值
的最大值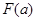 的解析式
的解析式
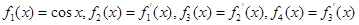 ,
,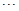
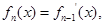 则
则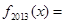 ( )
( )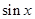
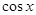
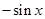
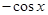
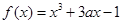 ,
, ,其中
,其中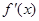 是
是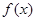 的导函数.
的导函数.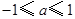 的一切
的一切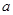 的值,都有
的值,都有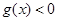 ,求实数
,求实数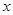 的取值范围;
的取值范围;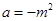 ,当实数
,当实数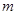 在什么范围内变化时,函数
在什么范围内变化时,函数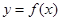 的图象与直线
的图象与直线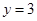 只有一个公共点.
只有一个公共点.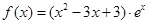 .
.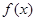 的单调区间;
的单调区间;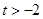 时,判断
时,判断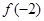 和
和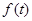 的大小,并说明理由;
的大小,并说明理由;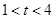 时,关于
时,关于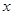 的方程:
的方程: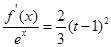 在区间
在区间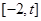 上总有两个不同的解.
上总有两个不同的解.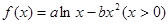
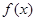 在x=1处与直线
在x=1处与直线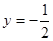 相切.
相切.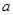 ,
,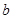 的值;②求函数
的值;②求函数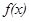 在
在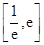 上的最大值.
上的最大值.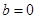 时,若不等式
时,若不等式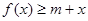 对所有的
对所有的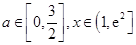 都成立,求实数
都成立,求实数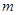 的取值范围.
的取值范围.