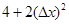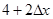题目内容
已知函数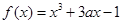 ,
, ,其中
,其中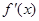 是
是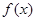 的导函数.
的导函数.
(1)对满足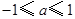 的一切
的一切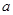 的值,都有
的值,都有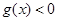 ,求实数
,求实数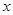 的取值范围;
的取值范围;
(2)设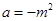 ,当实数
,当实数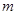 在什么范围内变化时,函数
在什么范围内变化时,函数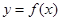 的图象与直线
的图象与直线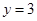 只有一个公共点.
只有一个公共点.
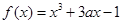 ,
, ,其中
,其中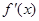 是
是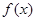 的导函数.
的导函数.(1)对满足
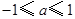 的一切
的一切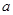 的值,都有
的值,都有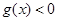 ,求实数
,求实数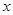 的取值范围;
的取值范围;(2)设
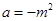 ,当实数
,当实数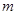 在什么范围内变化时,函数
在什么范围内变化时,函数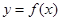 的图象与直线
的图象与直线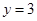 只有一个公共点.
只有一个公共点.(1)
(2)

(2)

试题分析:解:(1)由题意,得
 ,
,设
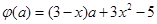 ,
,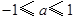 .
.对
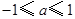 中任意
中任意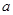 值,恒有
值,恒有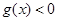 ,即
,即 ,
, 即
即
解得
 .
.故
 时,对满足
时,对满足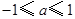 的一切
的一切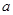 的值,都有
的值,都有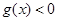 ;
;(2)
 ,
,①当
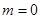 时,
时, 的图象与直线
的图象与直线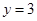 只有一个公共点;
只有一个公共点;②当
 时,列表:
时,列表: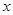 |  |  |  |  |  |
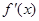 | 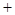 |  | 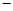 |  | 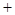 |
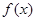 |  | 极大值 |  | 极小值 |  |
 ,
,又
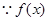 的值域是
的值域是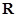 ,且在
,且在 上单调递增,
上单调递增, 当
当 时,函数
时,函数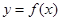 的图象与直线
的图象与直线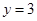 只有一个公共点,
只有一个公共点,当
 时,恒有
时,恒有 ,
,由题意,得
 ,
,即
 ,
,解得
 ,
,综上,
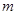 的取值范围是
的取值范围是 .
.点评:主要是考查了导数在研究函数单调性,以及根据函数与方程的思想来研究方程的解,属于中档题。

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 函数
函数
 图像以
图像以 为对称中心,求实数
为对称中心,求实数 和
和 的值
的值 ,求函数
,求函数 上的最小值
上的最小值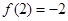 ,
,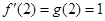 ,
,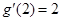 ,则函数
,则函数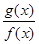 在
在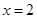 处的导数值为( )
处的导数值为( )



 且
且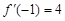 ,则实数
,则实数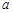 的值等于 ;
的值等于 ; 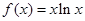
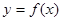 的图像在
的图像在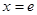 处的切线方程;
处的切线方程;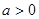 ,求函数
,求函数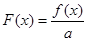 在
在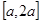 上的最小值.
上的最小值.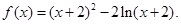
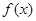 的单调区间;
的单调区间;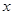 的方程
的方程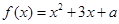 在区间
在区间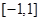 上有唯一实根,求实数
上有唯一实根,求实数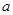 的取值范围.
的取值范围.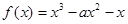 ;
;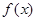 在
在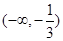 上单调递增,在
上单调递增,在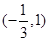 上单调递减,在
上单调递减,在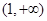 上单调递增,求实数
上单调递增,求实数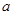 的值;
的值;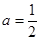 时,求证:当
时,求证:当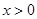 时,
时,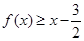 .
.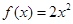 的图像上点P(1,2)及邻近点Q(
的图像上点P(1,2)及邻近点Q( ,
,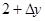 )则
)则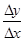 的值为
的值为