题目内容
已知函数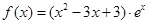 .
.
(1)求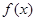 的单调区间;
的单调区间;
(2)当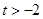 时,判断
时,判断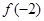 和
和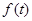 的大小,并说明理由;
的大小,并说明理由;
(3)求证:当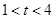 时,关于
时,关于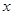 的方程:
的方程: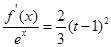 在区间
在区间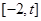 上总有两个不同的解.
上总有两个不同的解.
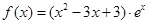 .
.(1)求
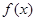 的单调区间;
的单调区间;(2)当
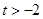 时,判断
时,判断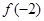 和
和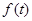 的大小,并说明理由;
的大小,并说明理由;(3)求证:当
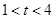 时,关于
时,关于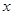 的方程:
的方程: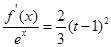 在区间
在区间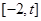 上总有两个不同的解.
上总有两个不同的解.(1)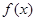 的单调递增区间为
的单调递增区间为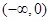 ,
, ,单调递减区间为
,单调递减区间为
(2)当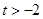 时,
时,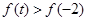 .
.
(3)构造函数 ,然后借助于
,然后借助于 在区间
在区间 、
、 分别存在零点,又由二次函数的单调性可知最多在两个零点,进而得到结论。
分别存在零点,又由二次函数的单调性可知最多在两个零点,进而得到结论。
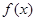 的单调递增区间为
的单调递增区间为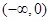 ,
, ,单调递减区间为
,单调递减区间为
(2)当
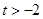 时,
时,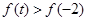 .
.(3)构造函数
 ,然后借助于
,然后借助于 在区间
在区间 、
、 分别存在零点,又由二次函数的单调性可知最多在两个零点,进而得到结论。
分别存在零点,又由二次函数的单调性可知最多在两个零点,进而得到结论。试题分析:(1)

当
 时可解得
时可解得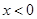 ,或
,或
当
 时可解得
时可解得
所以函数
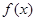 的单调递增区间为
的单调递增区间为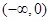 ,
, ,
,单调递减区间为
 3分
3分(2)当
 时,因为
时,因为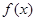 在
在 单调递增,所以
单调递增,所以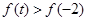
当
 时,因为
时,因为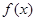 在
在 单减,在
单减,在 单增,
单增, 所能取得的最小值为
所能取得的最小值为 ,
,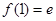 ,
, ,
, ,所以当
,所以当 时,
时,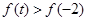 .
.综上可知:当
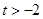 时,
时,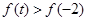 . 7分
. 7分(3)
 即
即
考虑函数
 ,
, ,
, ,
,
所以
 在区间
在区间 、
、 分别存在零点,又由二次函数的单调性可知:
分别存在零点,又由二次函数的单调性可知: 最多存在两个零点,所以关于
最多存在两个零点,所以关于 的方程:
的方程: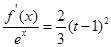 在区间
在区间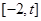 上总有两个不同的解 10分
上总有两个不同的解 10分点评:考查了导数在研究函数中的运用,以及利用函数与方程的思想的综合运用,属于难度题。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
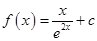 (
(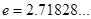 是自然对数的底数,
是自然对数的底数,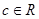 ).
).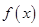 的单调区间、最大值;
的单调区间、最大值;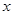 的方程
的方程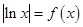 根的个数。
根的个数。 ,记
,记
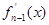 ,
, 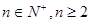 ).则
).则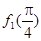 +
+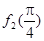 +…+
+…+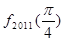 =
= 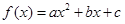 和“伪二次函数”
和“伪二次函数” 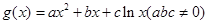 .
.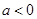 ,无论
,无论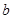 取何值,函数
取何值,函数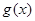 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;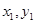 ),B(
),B(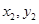 ),线段AB中点为C(
),线段AB中点为C(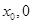 ),记直线AB的斜率为k.
),记直线AB的斜率为k.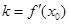 ;
;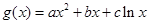 ,是否有(1)同样的性质?证明你的结论。
,是否有(1)同样的性质?证明你的结论。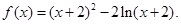
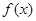 的单调区间;
的单调区间;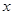 的方程
的方程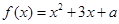 在区间
在区间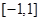 上有唯一实根,求实数
上有唯一实根,求实数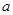 的取值范围.
的取值范围.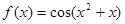 导数是( )
导数是( )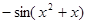

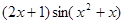
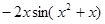
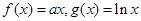 ,其中
,其中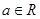 。
。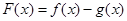 有极值
有极值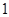 ,求
,求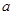 的值;
的值;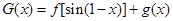 在区间
在区间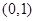 上为增函数,求
上为增函数,求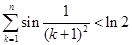
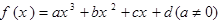 的对称中心为M
的对称中心为M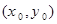 ,记函数
,记函数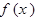 的导函数为
的导函数为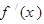 ,
, 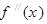 ,则有
,则有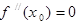 .若函数
.若函数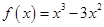 ,则可求得:
,则可求得: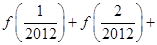
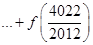
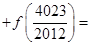 .
.