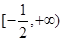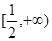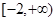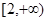题目内容
已知函数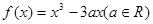
(1)当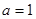 时,求
时,求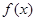 在
在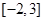 的最小值;
的最小值;
(2)若直线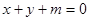 对任意的
对任意的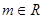 都不是曲线
都不是曲线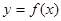 的切线,求
的切线,求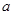 的取值范围;
的取值范围;
(3)设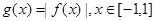 ,求
,求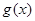 的最大值
的最大值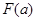 的解析式
的解析式
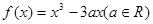
(1)当
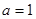 时,求
时,求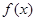 在
在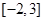 的最小值;
的最小值;(2)若直线
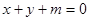 对任意的
对任意的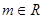 都不是曲线
都不是曲线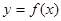 的切线,求
的切线,求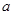 的取值范围;
的取值范围;(3)设
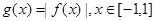 ,求
,求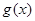 的最大值
的最大值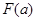 的解析式
的解析式
(1)-2
(2)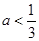
(3)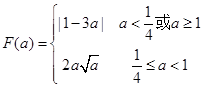
(2)
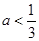
(3)
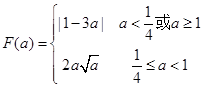
试题分析:解:(1)
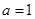 时,
时,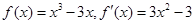
令
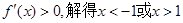
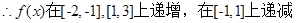 2分
2分又
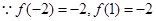 ,
,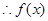 在
在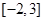 的最小值为-2 4分
的最小值为-2 4分(2)直线的斜率为-1,由题意,方程
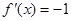 无实数解 6分
无实数解 6分即
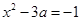 无实数解,即
无实数解,即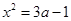 无实数解,
无实数解,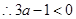 ,解得
,解得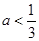 8分
8分(3)由题意
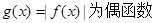 ,只需要求
,只需要求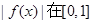 上的最大值
上的最大值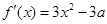 且
且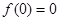
当
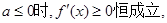
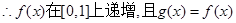
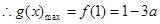 10分
10分当
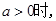 令
令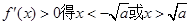
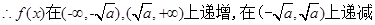
又由
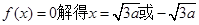 ,
,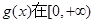 的图像如图所示
的图像如图所示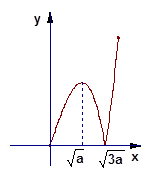
当
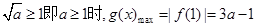 12分
12分当
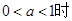 ,
,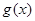 的最大值在
的最大值在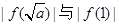 中取得
中取得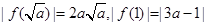
以下解不等式
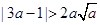
当
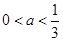 时,原不等式可化为
时,原不等式可化为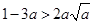
解得:
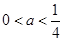
当
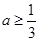 时,原不等式可化为
时,原不等式可化为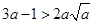 ,此式无解
,此式无解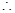 当
当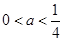 时,
时,
当
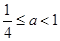 时,
时,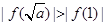 14分
14分综上:
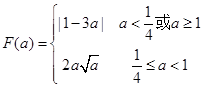 16分
16分点评:主要是考查了导数几何意义以及导数判定函数单调性以及最值的运用,属于中档题。

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
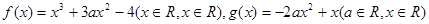 (Ⅰ)若函数
(Ⅰ)若函数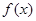 在
在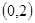 上单调递减,在区间
上单调递减,在区间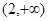 单调递增,求
单调递增,求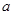 的值;
的值;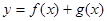 在
在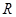 上有两个不同的极值点,求
上有两个不同的极值点,求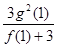 的取值范围;
的取值范围;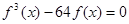 有且只有三个不同的实根,求
有且只有三个不同的实根,求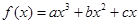 在点
在点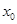 处取得极小值-4,使其导数
处取得极小值-4,使其导数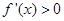 的
的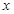 的取值范围为
的取值范围为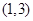 ,求:
,求: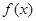 的解析式;
的解析式;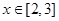 ,求
,求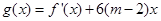 的最大值;
的最大值;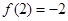 ,
,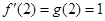 ,
,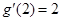 ,则函数
,则函数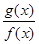 在
在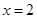 处的导数值为( )
处的导数值为( )



 ,记
,记
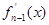 ,
, 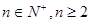 ).则
).则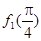 +
+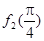 +…+
+…+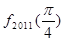 =
=  且
且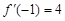 ,则实数
,则实数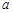 的值等于 ;
的值等于 ; 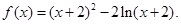
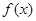 的单调区间;
的单调区间;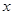 的方程
的方程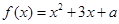 在区间
在区间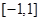 上有唯一实根,求实数
上有唯一实根,求实数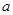 的取值范围.
的取值范围.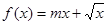 在区间
在区间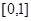 单调递增,则m的取值范围为
单调递增,则m的取值范围为