题目内容
已知函数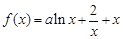 ,其中
,其中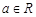 .
.
(1)若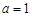 ,求函数
,求函数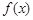 的极值点;
的极值点;
(2)若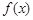 在区间
在区间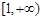 内单调递增,求实数
内单调递增,求实数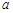 的取值范围.
的取值范围.
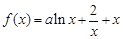 ,其中
,其中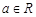 .
.(1)若
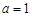 ,求函数
,求函数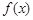 的极值点;
的极值点;(2)若
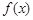 在区间
在区间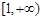 内单调递增,求实数
内单调递增,求实数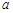 的取值范围.
的取值范围.(1)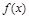 有极小值点
有极小值点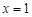 ,无极大值点;(2)[1,+∞)。
,无极大值点;(2)[1,+∞)。
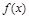 有极小值点
有极小值点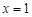 ,无极大值点;(2)[1,+∞)。
,无极大值点;(2)[1,+∞)。试题分析:(1)先求出函数的定义域,求出函数的导数,求出导数为0的点,确定导数为0和导数不存在点的点的左右两侧导函数的符号,确定函数的单调性,若单调性相同不是极值点,若左增右减是极大值点,若左减右增是极小值点;(2)先求出导数,利用导数与函数单调性关系,将函数在[1,+∞)上是增函数问题转化为导函数大于等于0在[1,+∞)上恒成立问题,通过参变分离,转化为
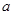 ≥
≥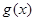 在[1,+∞)恒成立问题,求出
在[1,+∞)恒成立问题,求出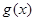 在[1,+∞)的最大值
在[1,+∞)的最大值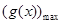 ,则
,则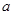 ≥
≥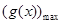 .
.试题解析:(1)当
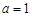 时,
时,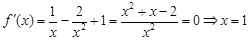 或
或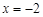 ……3分
……3分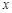 | 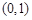 | 1 | 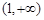 |
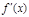 | 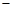 | 0 |  |
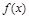 | 单调减 | 极小值 | 单调增 |
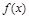 有极小值点
有极小值点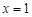 ,无极大值点……6分
,无极大值点……6分(2)
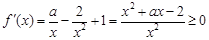 ,所以
,所以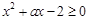
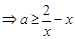 对
对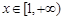 恒成立……9分
恒成立……9分又
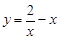 在
在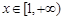 上单调递减,所以
上单调递减,所以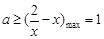 .……12分
.……12分
练习册系列答案
相关题目
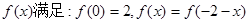 ,它的导函数的图象与直线
,它的导函数的图象与直线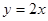 平行.
平行.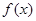 的解析式;
的解析式;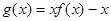 的图象与直线
的图象与直线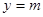 有三个公共点,求m的取值范围.
有三个公共点,求m的取值范围.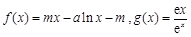 ,其中m,a均为实数.
,其中m,a均为实数.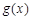 的极值;
的极值;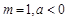 ,若对任意的
,若对任意的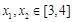
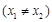 ,
,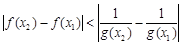 恒成立,求
恒成立,求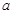 的最小值;
的最小值;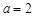 ,若对任意给定的
,若对任意给定的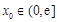 ,在区间
,在区间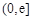 上总存在
上总存在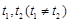 ,使得
,使得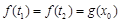 成立,求
成立,求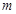 的取值范围.
的取值范围. .
.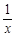 -(2+a)lnx(a≥0).
-(2+a)lnx(a≥0).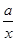 .
.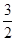 ,求实数a的值;
,求实数a的值;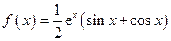 在区间
在区间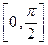 上的值域为( )
上的值域为( )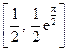
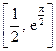
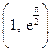
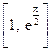
 的图象如图所示(其中
的图象如图所示(其中 是函数
是函数 的导函数).下面四个图象中,
的导函数).下面四个图象中, 的图象大致是( )
的图象大致是( )




