题目内容
【题目】设函数f(x)= ![]() (其中常数a>0,且a≠1).
(其中常数a>0,且a≠1).
(1)当a=10时,解关于x的方程f(x)=m(其中常数m>2 ![]() );
);
(2)若函数f(x)在(﹣∞,2]上的最小值是一个与a无关的常数,求实数a的取值范围.
【答案】
(1)解:f(x)= 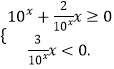
①当x<0时,f(x)= ![]() >3.因为m>2
>3.因为m>2 ![]() .
.
则当2 ![]() <m≤3时,方程f(x)=m无解;
<m≤3时,方程f(x)=m无解;
当m>3,由10x= ![]() ,得x=lg
,得x=lg ![]() .
.
②当x≥0时,10x≥1.由f(x)=m得10x+ ![]() =m,
=m,
∴(10x)2﹣m10x+2=0.
因为m>2 ![]() ,判别式△=m2﹣8>0,解得10x=
,判别式△=m2﹣8>0,解得10x= ![]() .
.
因为m>2 ![]() ,所以
,所以 ![]() >
> ![]() >1.
>1.
所以由10x= ![]() ,解得x=lg
,解得x=lg ![]() .
.
令 ![]() =1,得m=3.
=1,得m=3.
所以当m>3时, ![]() =
= ![]() <
< ![]() =1,
=1,
当2 ![]() <m≤3时,
<m≤3时, ![]() =
= ![]() >
> ![]() =1,解得x=lg
=1,解得x=lg ![]() .
.
综上,当m>3时,方程f(x)=m有两解x=lg ![]() 和x=lg
和x=lg ![]() ;
;
当2 ![]() <m≤3时,方程f(x)=m有两解x=lg
<m≤3时,方程f(x)=m有两解x=lg ![]() .
.
(2)解:①若0<a<1,
当x<0时,0<f(x)= ![]() <3;
<3;
当0≤x≤2时,f(x)=ax+ ![]() .
.
令t=ax,则t∈[a2,1],g(t)=t+ ![]() 在[a2,1]上单调递减,
在[a2,1]上单调递减,
所以当t=1,即x=0时f(x)取得最小值为3.
当t=a2时,f(x)取得最大值为 ![]() .
.
此时f(x)在(﹣∞,2]上的值域是(0, ![]() ],没有最小值.
],没有最小值.
②若a>1,
当x<0时,f(x)= ![]() >3;
>3;
当0≤x≤2时f(x)=ax+ ![]() .
.
令t=ax,g(t)=t+ ![]() ,则t∈[1,a2].
,则t∈[1,a2].
①若a2≤ ![]() ,g(t)=t+
,g(t)=t+ ![]() 在[1,a2]上单调递减,
在[1,a2]上单调递减,
所以当t=a2即x=2时f(x)取最小值a2+ ![]() ,最小值与a有关;
,最小值与a有关;
②a2> ![]() ,g(t)=t+
,g(t)=t+ ![]() 在[1,
在[1, ![]() ]上单调递减,在[
]上单调递减,在[ ![]() ,a2]上单调递增,
,a2]上单调递增,
所以当t= ![]() 即x=loga
即x=loga ![]() 时f(x)取最小值2
时f(x)取最小值2 ![]() ,最小值与a无关.
,最小值与a无关.
综上所述,当a≥ ![]() 时,f(x)在(﹣∞,2]上的最小值与a无关.
时,f(x)在(﹣∞,2]上的最小值与a无关.
【解析】(1)当a=10时,脱掉绝对值,写出f(x)的分段函数,根据分段函数在相应的区间所对应的解析式进行求解,(2)根据题意有![]() ,对a进行分类讨论,①a>1时,②0<a<1时,两种情况分析,每种情况下根据绝对值,再按照x≥0时,和-2≤x<0两种情况讨论,最后可得结论.
,对a进行分类讨论,①a>1时,②0<a<1时,两种情况分析,每种情况下根据绝对值,再按照x≥0时,和-2≤x<0两种情况讨论,最后可得结论.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案