题目内容
9.设点P是△ABC内一点(不包括边界),且$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$(m.n∈R),则m2+n2-2m-2n+3的取值范围是$(\frac{3}{2},3)$.分析 根据题意可得m、n满足的不等式组,在mon坐标系内作出不等式组对应的平面区域,利用线性规划,结合两点间的距离是即可得到结论.
解答 解:∵点P是△ABC内一点(不包括边界),$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,(m.n∈R),
∴实数m、n满足不等式组$\left\{\begin{array}{l}{m>0}\\{n>0}\\{m+n<1}\end{array}\right.$,
在mon坐标系内作出不等式组表示的平面区域,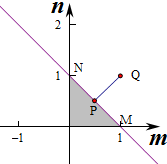
得到如图所示的△MN0内部(不含边界),其中M(1,0),N(0,1),O是坐标原点.
∵m2+n2-2m-2n+3=(m-1)2+(n-1)2+1.
设P(m,n)是区域内一点,Q(1,1)
∵|PQ|=$\sqrt{(m-1)^{2}+(n-1)^{2}}$,
∴z=(m-1)2+(n-1)2+1表示P、Q连线段长的平方加1.
运动点P,可得当P与Q在MN上的射影重合时,|PQ|达到最小值,
当P与原点O重合时,|PQ|达到最大值.
∵点P到MN的距离为d1=$\frac{|1+1-1|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,|PO|=$\sqrt{{(0-1)}^{2}+{(0-1)}^{2}}$=$\sqrt{2}$,
∴(m-1)2+(n-1)2∈($({\frac{\sqrt{2}}{2})}^{2}$,$({\sqrt{2})}^{2}$),
即(m-1)2+(n-1)2的取值范围是$(\frac{1}{2},2)$.
则z=(m-1)2+(n-1)2+1∈$(\frac{3}{2},3)$
故答案为:$(\frac{3}{2},3)$
点评 本题主要考查线性规划的应用,以平面向量为载体,求(m-1)2+(n-1)2+1的取值范围.着重考查了向量的线性运算、二元一次不等式组表示的平面区域和点到直线的距离公式等知识,综合性较强,难度较大.

| A. | [-3,11] | B. | [-3,13] | C. | [-5,13] | D. | [-5,11] |
| A. | ($\frac{1}{4}$,1+$\frac{\sqrt{2}}{2}$] | B. | ($\frac{1}{4}$,1] | C. | ($\frac{1}{4}$,+∞) | D. | ($\frac{1}{2}$,+∞) |
 一个圆柱形的罐子半径是4米,高是9米,将其水平躺倒,并在其中注入深2米的水,截面如图所示,水的体积是( )立方米.
一个圆柱形的罐子半径是4米,高是9米,将其水平躺倒,并在其中注入深2米的水,截面如图所示,水的体积是( )立方米.| A. | 24$π-24\sqrt{3}$ | B. | 36$π-36\sqrt{3}$ | C. | 36$π-24\sqrt{3}$ | D. | 48$π-36\sqrt{3}$ |
| A. | 24种 | B. | 48种 | C. | 120种 | D. | 124种 |
 如图,平面四边形EFGH的四个顶点分别在空间四边形ABCD的四条边上,若直线EF与GH相交,则它们的交点M必在直线AC上.
如图,平面四边形EFGH的四个顶点分别在空间四边形ABCD的四条边上,若直线EF与GH相交,则它们的交点M必在直线AC上.