题目内容
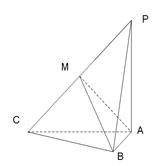
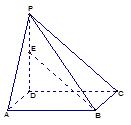
如图3,三棱锥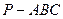 中,
中,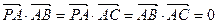 ,
,
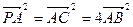 .(1)求证:
.(1)求证: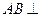 平面
平面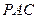 ;
;
(2)若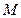 为线段
为线段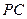 上的点,设
上的点,设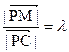 ,问
,问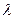 为何值时,
为何值时,
能使直线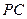
 平面
平面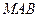 ?
?
(3)求二面角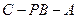 的平面角的余弦值 图3
的平面角的余弦值 图3
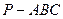 中,
中,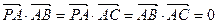 ,
,
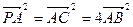 .(1)求证:
.(1)求证: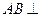 平面
平面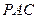 ;
;(2)若
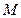 为线段
为线段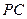 上的点,设
上的点,设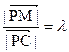 ,问
,问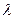 为何值时,
为何值时,能使直线
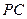
 平面
平面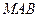 ?
?(3)求二面角
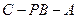 的平面角的余弦值 图3
的平面角的余弦值 图3(1)略 (2)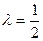 (3)
(3)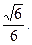
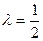 (3)
(3)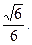
:(1)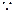
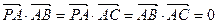 ,
,
∴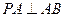 ,
,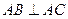 ,
,
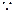
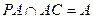 ,
,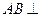 平面
平面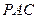 .…………3分
.…………3分
(2)如图,以A为坐标原点,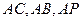 所在直线分别为
所在直线分别为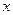 轴,
轴,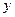 轴,
轴, 轴建立空间直角坐标系.设
轴建立空间直角坐标系.设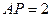 ,则
,则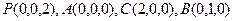 .
.
当M为PC中点时,即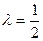 时,直线
时,直线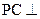 平面
平面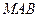 .
.
 证明如下:当M为PC中点时,
证明如下:当M为PC中点时, .
.
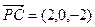 ,
,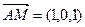 ,
,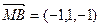 .
.
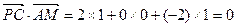 ,
,
∴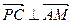 ,即
,即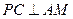 .
.
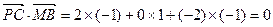 ,
,
∴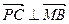 ,即
,即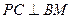 .又
.又 ,∴
,∴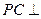 平面
平面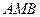 .
.
(3)可证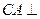 平面
平面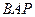 .则平面
.则平面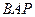 法向量为
法向量为 ,
,
下面求平面PBC的法向量.设平面PBC的法向量为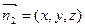 ,
,
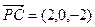 ,
,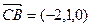 ,
,
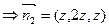 。
。
令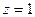 ,则
,则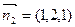 ,
,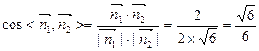 。
。
所以二面角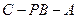 的平面角的余弦值是
的平面角的余弦值是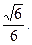 …13分
…13分
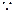
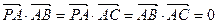 ,
,∴
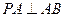 ,
,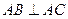 ,
,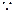
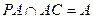 ,
,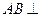 平面
平面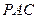 .…………3分
.…………3分(2)如图,以A为坐标原点,
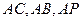 所在直线分别为
所在直线分别为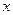 轴,
轴,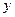 轴,
轴, 轴建立空间直角坐标系.设
轴建立空间直角坐标系.设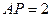 ,则
,则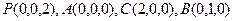 .
. 当M为PC中点时,即
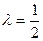 时,直线
时,直线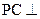 平面
平面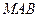 .
.  证明如下:当M为PC中点时,
证明如下:当M为PC中点时, .
.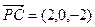 ,
,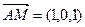 ,
,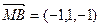 .
.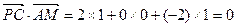 ,
, ∴
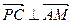 ,即
,即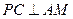 .
. 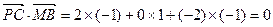 ,
, ∴
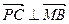 ,即
,即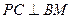 .又
.又 ,∴
,∴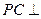 平面
平面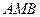 .
.(3)可证
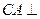 平面
平面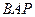 .则平面
.则平面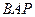 法向量为
法向量为 ,
, 下面求平面PBC的法向量.设平面PBC的法向量为
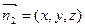 ,
,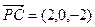 ,
,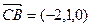 ,
,
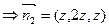 。
。令
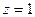 ,则
,则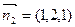 ,
,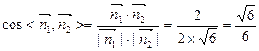 。
。 所以二面角
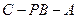 的平面角的余弦值是
的平面角的余弦值是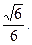 …13分
…13分
练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
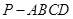 中,底面
中,底面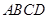 是正方形,
是正方形,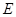 为
为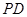 中点,若
中点,若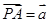 ,
,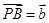 ,
,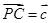 ,则
,则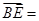 ( *** )
( *** )
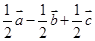
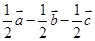
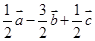
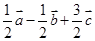
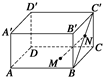
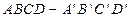 的棱长为a,M为
的棱长为a,M为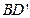 的中点,点N在
的中点,点N在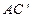 上,且
上,且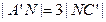 ,试求MN的长.
,试求MN的长.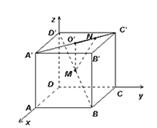
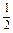
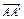 +
+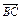 +
+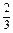
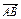 ,并在图上标出其结果;
,并在图上标出其结果;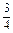 分点,设
分点,设 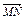 =
=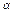
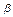
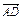 +
+
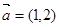 ,
,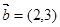 ,若向量
,若向量 与向量
与向量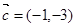 共线,则
共线,则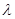 = .
= .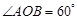 ,C为弧AB上的一个动点.若
,C为弧AB上的一个动点.若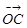
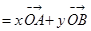 ,则
,则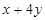 的取值范围是 .
的取值范围是 .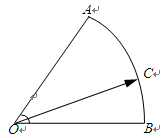
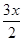 ,sin
,sin 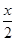 ,-cos
,-cos 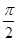 ,π].
,π].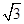 ,求x的值;
,求x的值;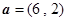 ,b=(-2,4),则a+b= _______.
,b=(-2,4),则a+b= _______.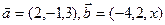 ,若
,若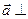
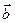 ,则
,则 ______;若
______;若