题目内容
已知向量a=(cos 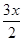 ,sin
,sin 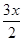 ),b=(-sin
),b=(-sin 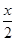 ,-cos
,-cos 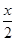 ),其中x∈[
),其中x∈[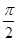 ,π].
,π].
(1)若|a+b|=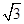 ,求x的值;
,求x的值;
(2)函数f(x)=a·b+|a+b|2,若c>f(x)恒成立,求实数c的取值范围.
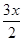 ,sin
,sin 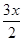 ),b=(-sin
),b=(-sin 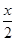 ,-cos
,-cos 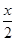 ),其中x∈[
),其中x∈[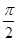 ,π].
,π].(1)若|a+b|=
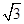 ,求x的值;
,求x的值;(2)函数f(x)=a·b+|a+b|2,若c>f(x)恒成立,求实数c的取值范围.
(1)x= 或x=
或x=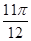 (2)(5,+∞)
(2)(5,+∞)
 或x=
或x=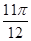 (2)(5,+∞)
(2)(5,+∞)(1)∵a+b=(cos 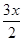 -sin
-sin 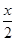 ,sin
,sin 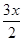 -cos
-cos 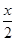 ),
),
∴|a+b|= =
=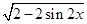 ,
,
由|a+b|=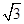 ,得
,得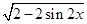 =
=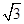 ,即sin 2x=-
,即sin 2x=-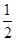 .
.
∵x∈[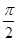 ,π],∴π≤2x≤2π.
,π],∴π≤2x≤2π.
因此2x=π+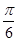 或2x=2π-
或2x=2π-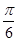 ,即x=
,即x= 或x=
或x=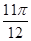 .
.
(2)∵a·b=-cos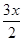 sin
sin 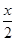 -sin
-sin 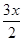 cos
cos 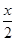 =-sin 2x,
=-sin 2x,
∴f(x)=a·b+|c+b|2=2-3sin 2x,
∵π≤2x≤2π,∴-1≤sin 2x≤0,
∴2≤f(x)=2-3sin 2x≤5,∴[f(x)]max=5.
又c>f(x)恒成立,
因此c>[f(x)]max,则c>5.
∴实数c的取值范围为(5,+∞).
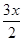 -sin
-sin 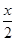 ,sin
,sin 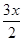 -cos
-cos 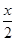 ),
),∴|a+b|=
 =
=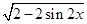 ,
,由|a+b|=
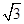 ,得
,得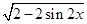 =
=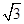 ,即sin 2x=-
,即sin 2x=-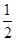 .
.∵x∈[
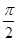 ,π],∴π≤2x≤2π.
,π],∴π≤2x≤2π.因此2x=π+
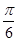 或2x=2π-
或2x=2π-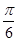 ,即x=
,即x= 或x=
或x=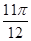 .
.(2)∵a·b=-cos
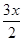 sin
sin 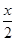 -sin
-sin 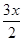 cos
cos 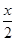 =-sin 2x,
=-sin 2x,∴f(x)=a·b+|c+b|2=2-3sin 2x,
∵π≤2x≤2π,∴-1≤sin 2x≤0,
∴2≤f(x)=2-3sin 2x≤5,∴[f(x)]max=5.
又c>f(x)恒成立,
因此c>[f(x)]max,则c>5.
∴实数c的取值范围为(5,+∞).

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
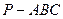 中,
中,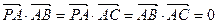 ,
,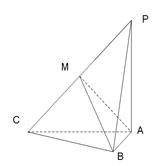
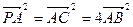 .(1)求证:
.(1)求证: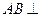 平面
平面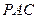 ;
;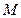 为线段
为线段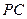 上的点,设
上的点,设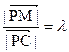 ,问
,问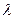 为何值时,
为何值时, 平面
平面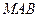 ?
?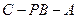 的平面角的余弦值 图3
的平面角的余弦值 图3 ,向量
,向量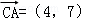 ,则
,则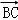 =( )
=( ) ,
, 满足
满足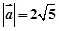 ,
, 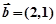 ,且
,且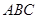 的顶点坐标分别为
的顶点坐标分别为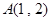 ,
,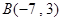 ,点
,点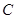 在直线
在直线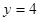 上运动,
上运动,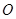 为坐标原点,
为坐标原点,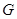 为△
为△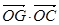 的最小值为__________.
的最小值为__________.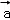 =(2,1),
=(2,1),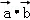 =10,|
=10,|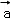 +
+ |=
|=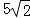 ,则|
,则|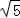

 同方向的单位向量为( )
同方向的单位向量为( )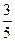 ,-
,-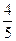 )
)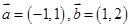 ,且
,且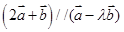 ,则
,则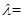 .
.