题目内容
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的极值;
的极值;
(2)问:是否存在实数![]() ,使得
,使得![]() 有两个相异零点?若存在,求出
有两个相异零点?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1) ①当![]() 时,函数
时,函数![]() 无极值.②当
无极值.②当![]() 时,函数
时,函数![]() 有极小值为
有极小值为![]() ,无极大值;(2)存在,
,无极大值;(2)存在,![]()
【解析】
(1)对函数![]() 求导,根据
求导,根据![]() 的不同取值范围,进行分类讨论,求出函数
的不同取值范围,进行分类讨论,求出函数![]() 的极值;
的极值;
(2)根据![]() 的不同取值范围,进行分类讨论,结合
的不同取值范围,进行分类讨论,结合![]() 、函数的极值的大小、(1)中的结论,最后求出
、函数的极值的大小、(1)中的结论,最后求出![]() 的取值范围.
的取值范围.
解:(1)因为![]() ,所以
,所以![]() .
.
①当![]() 时,
时,![]() ,
,
所以![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减.
上单调递减.
此时,函数![]() 无极值.
无极值.
②当![]() 时,令
时,令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增.
上单调递增.
此时,函数![]() 有极小值为
有极小值为![]() ,无极大值.
,无极大值.
(2)存在实数![]() ,使得
,使得![]() 有两个相异零点.
有两个相异零点.
由(1)知:①当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减;
上单调递减;
又![]() ,所以此时函数
,所以此时函数![]() 仅有一个零点;
仅有一个零点;
②当![]() 时,
时,![]() .
.
因为![]() ,则由(1)知
,则由(1)知![]() ;
;
取![]() ,令
,令![]() ,
,
易得![]() ,所以
,所以![]() 在
在![]() 单调递减,
单调递减,
所以![]() ,所以
,所以![]() .
.
此时,函数![]() 在
在![]() 上也有一个零点.
上也有一个零点.
所以,当![]() 时,函数
时,函数![]() 有两个相异零点.
有两个相异零点.
③当![]() 时,
时,![]() ,
,![]() ,
,
此时函数![]() 仅有一个零点.
仅有一个零点.
④当![]() 时,
时,![]() ,因为
,因为![]() ,则由(1)知
,则由(1)知![]() ;
;
令函数![]() ,易得
,易得![]() ,
,
所以![]() ,所以
,所以![]() ,即
,即![]() .
.
又![]() ,所以函数
,所以函数![]() 在
在![]() 上也有一个零点,
上也有一个零点,
所以,当![]() 时,函数
时,函数![]() 有两个相异零点.
有两个相异零点.
综上所述,当![]() 时,函数
时,函数![]() 有两个相异零点.
有两个相异零点.

 巧学巧练系列答案
巧学巧练系列答案【题目】某学校数学建模小组为了研究双层玻璃窗户中每层玻璃厚度![]() (每层玻璃的厚度相同)及两层玻璃间夹空气层厚度
(每层玻璃的厚度相同)及两层玻璃间夹空气层厚度![]() 对保温效果的影响,利用热传导定律得到热传导量
对保温效果的影响,利用热传导定律得到热传导量![]() 满足关系式:
满足关系式: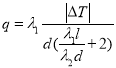 ,其中玻璃的热传导系数
,其中玻璃的热传导系数![]() 焦耳/(厘米
焦耳/(厘米![]() 度),不流通、干燥空气的热传导系数
度),不流通、干燥空气的热传导系数![]() 焦耳/(厘米
焦耳/(厘米![]() 度),
度), ![]() 为室内外温度差.
为室内外温度差.![]() 值越小,保温效果越好.现有4种型号的双层玻璃窗户,具体数据如下表:
值越小,保温效果越好.现有4种型号的双层玻璃窗户,具体数据如下表:
型号 | 每层玻璃厚度 (单位:厘米) | 玻璃间夹空气层厚度 (单位:厘米) |
A型 |
|
|
B型 |
|
|
C型 |
|
|
D型 |
|
|
则保温效果最好的双层玻璃的型号是________型.