题目内容
【题目】已知椭圆
上的焦点为
，离心率为
．
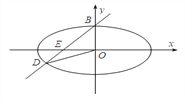
（1）求椭圆方程；
（2）设过椭圆顶点
，斜率为
的直线交椭圆于另一点
，交
轴于点
，且
， 
， 
成等比数列，求
的值．
【答案】(1) 椭圆的方程为
;(2)当
， 
， 
成等比数列时， 
.
【解析】试题分析：（Ⅰ）由椭圆的性质容易求出参数a,b的值，从而求出椭圆方程；（Ⅱ）设出直线方程，代入椭圆方程，求出点D、E的坐标，然后利用|BD|，|BE|，|DE|成等比数列，即可求解．
试题解析：（Ⅰ）由已知
．解得
，所以
，椭圆的方程为
．
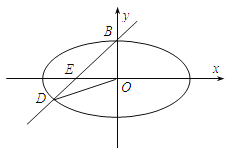
（Ⅱ）由（Ⅰ）得过B点的直线为
，由
得
，所以
，所以
，依题意
．因为|BD|，|BE|，|DE|成等比数列，所以
，所以
，即
，当
时， 
，无解，当
时， 
，解得
，所以，当|BD|，|BE|，|DE|成等比数列时， 
．
练习册系列答案
名校课堂系列答案
相关题目
