题目内容
【题目】已知函数f(x)=![]() g(x)=f(x)+
g(x)=f(x)+![]() x-6lnx,其中
x-6lnx,其中![]() R.
R.
(1)当![]() =1时,判断f(x)的单调性;
=1时,判断f(x)的单调性;
(2)当![]() =2时,求出g(x)在(0,1)上的最大值;
=2时,求出g(x)在(0,1)上的最大值;
(3)设函数![]() 当
当![]() =2时,若
=2时,若![]() 总有
总有![]() 成立,求实数m的取值范围.
成立,求实数m的取值范围.
【答案】(1)f(x)在![]() 上单调递增;(2)
上单调递增;(2)![]() ;(3)[8-5
;(3)[8-5![]() .
.
【解析】
(1)当![]() 时,利用函数的导数可判断出函数在
时,利用函数的导数可判断出函数在![]() 上递增.(2)当
上递增.(2)当![]() 时,利用
时,利用![]() 的导数求得函数的单调区间,进而求得函数的最大值.(3)将原不等式成立转化为
的导数求得函数的单调区间,进而求得函数的最大值.(3)将原不等式成立转化为![]() 来求解,根据(2)的结论以及二次函数
来求解,根据(2)的结论以及二次函数![]() 在
在![]() 上的最大值列不等式组,解不等式组求得
上的最大值列不等式组,解不等式组求得![]() 的取值范围.
的取值范围.
(1)由题意知f(x)的定义域为![]()
f′![]() .
.
当a=1时,在![]() 上,f′
上,f′![]()
故f(x)在![]() 上单调递增.
上单调递增.
(2)由![]() lnx,当a=2时
lnx,当a=2时![]() lnx,
lnx,
g′![]() 由g′(x)=0,得
由g′(x)=0,得![]() 或x=2.
或x=2.
当![]() 时,g′(x)>0;当
时,g′(x)>0;当![]() 时,g′(x)<0
时,g′(x)<0
所以在(0,1)内![]() ln2.
ln2.
(3)”![]() 总有
总有![]() 成立”等价于”g(x)在(0,1)内的最大值不小于h(x)在[1,2]上的最大值”,而h(x)在[1,2]上的最大值为max{h(1),h(2)},
成立”等价于”g(x)在(0,1)内的最大值不小于h(x)在[1,2]上的最大值”,而h(x)在[1,2]上的最大值为max{h(1),h(2)},
所以有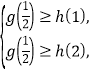 即
即![]()
可得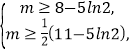 即
即![]() ln2,
ln2,
所以实数m的取值范围是[8-5![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】如图,在三棱台ABCDEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.

(1)求证:BF⊥平面ACFD;
(2)求二面角B-AD-F的平面角的余弦值.
【题目】近年来,我国电子商务蓬勃发展,有关部门推出了针对网购平台的商品和服务的评价系统,从该系统中随机选出100名交易者,并对其交易评价进行了统计,网购者对商品的满意率为0.6,对服务的满意率为0.75,其中对商品和服务都满意的有40人.
(1)根据已知条件完成下面的![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“网购者对服务满意与对商品满意之间有关”?
的把握认为“网购者对服务满意与对商品满意之间有关”?
对服务满意 | 对服务不满意 | 合计 | |
对商品满意 |
| ||
对商品不满意 | |||
合计 |
|
(2)若对商品和服务都不满意者的集合为![]() .已知
.已知![]() 中有2名男性,现从
中有2名男性,现从![]() 中任取2人调查其意见.求取到的2人恰好是一男一女的概率.
中任取2人调查其意见.求取到的2人恰好是一男一女的概率.
附: 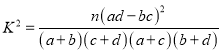 (其中
(其中![]() 为样本容量)
为样本容量)
|
|
|
|
|
|
|
|
|
|
