题目内容
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() ,(t为参数).
,(t为参数).
(1)若a=-1,求C与l的交点坐标;
(2)若C上的点到l距离的最大值为![]() ,求a.
,求a.
【答案】(1)![]() 和
和![]() ;(2)
;(2)![]() 或8
或8
【解析】试题分析:(1)将曲线C与直线l的参数方程转化为普通方程,解方程组即可;(2)l的参数方程化为一般方程是:x+4y﹣a﹣4=0,在椭圆C上的任一点P可以表示成P(3cosθ,sinθ),利用点到直线距离公式,转化为三角函数最值问题.
试题解析:
(1)曲线C的参数方程为![]() (θ为参数),化为标准方程是:
(θ为参数),化为标准方程是:![]() +y2=1;
+y2=1;
a=﹣1时,直线l的参数方程化为一般方程是:x+4y﹣3=0;
联立方程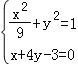 , 解得
, 解得![]() 或
或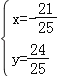 ,
,
所以椭圆C和直线l的交点为(3,0)和(﹣![]() ,
,![]() ).
).
(2)l的参数方程![]() (t为参数)化为一般方程是:x+4y﹣a﹣4=0,
(t为参数)化为一般方程是:x+4y﹣a﹣4=0,
椭圆C上的任一点P可以表示成P(3cosθ,sinθ),θ∈[0,2π),
所以点P到直线l的距离d为:
d=![]() =
=![]() ,φ满足tanφ=
,φ满足tanφ=![]() ,
,
又d的最大值dmax=![]() ,
,
所以|5sin(θ+φ)﹣a﹣4|的最大值为17,
得:5﹣a﹣4=17或﹣5﹣a﹣4=﹣17,
即a=﹣16或a=8.

练习册系列答案
相关题目