题目内容
12.已知△ABC中,a=3${\;}^{\frac{1}{2}}$,$\frac{b+c}{a}$=$\frac{2-cosB-cosC}{cosA}$,求三角形周长.分析 由$\frac{b+c}{a}$=$\frac{2-cosB-cosC}{cosA}$,由正弦定理可得:$\frac{sinB+sinC}{sinA}$=$\frac{2-cosB-cosC}{cosA}$,化为sinC+sinB=2sinA,由正弦定理可得:c+b=2a,即可得出.
解答 解:∵$\frac{b+c}{a}$=$\frac{2-cosB-cosC}{cosA}$,
由正弦定理可得:$\frac{sinB+sinC}{sinA}$=$\frac{2-cosB-cosC}{cosA}$,
化为sinBcosA+sinCcosA=2sinA-sinAcosB-sinAcosC,
∴sinBcosA+sinAcosB+sinAcosC+sinCcosA=2sinA,
∴sin(A+B)+sin(A+C)=2sinA,
即sinC+sinB=2sinA,
由正弦定理可得:c+b=2a,
∴三角形周长=a+b+c=3a=3$\sqrt{3}$.
点评 本题考查了正弦定理余弦定理、两角和差的正弦公式、三角形的周长计算,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
2.将函数f(x)=sin2x的图象向右平移φ(0<φ<$\frac{π}{2}$)个单位后得到函数g(x)的图象.若对满足|f(x1)-g(x2)|=2的x1、x2,有|x1-x2|min=$\frac{π}{3}$,则φ=( )
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
20.已知直线y=$\frac{1}{3}x+\frac{2}{3}$与幂函数f(x)=xm(m≠0)的图象将于A、B两点,且|AB|=$\sqrt{10}$,则m的值为( )
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
7.已知M是△ABC内一点,且$\overrightarrow{AB}$•$\overrightarrow{AC}$=2$\sqrt{3}$,∠BAC=30°,若△MBC,△MCA,△MAB的面积分别为$\frac{1}{2}$,x,y则xy的最大值是( )
| A. | $\frac{1}{14}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{20}$ |
4.已知定义在(-3,3)上的函数f(x)满足f(x-1)=-f(1-x),且x≥0时,f(x)=x3,则f(x)+27f(1-x)>0的解集为( )
| A. | ∅ | B. | (-3,$\frac{1}{2}$) | C. | (-2,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,3) |
2.某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( )
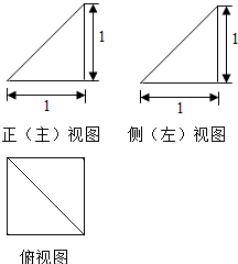

| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |