题目内容
3.已知A,B,C三点不重合,则“$\overrightarrow{AB}=\overrightarrow{BC}$”是“A,B,C三点共线”成立的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 根据三点共线的向量关系,根据充分条件和必要条件的定义进行判断.
解答 解:A,B,C三点不重合,若A,B,C三点共线”,则“$\overrightarrow{AB}$=λ$\overline{BC}$,λ≠0,λ为常数”
故“$\overrightarrow{AB}=\overrightarrow{BC}$”能推出“A,B,C三点共线”,但是“A,B,C三点共线”,λ为不等于0的常数,
故A,B,C三点不重合,则“$\overrightarrow{AB}=\overrightarrow{BC}$”是“A,B,C三点共线”成立的充分不必要条件.
故选:A.
点评 本题主要考查充分条件和必要条件的判断,根据三点关共线的等价条件是解决本题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
11.已知直线y=ax+1经过抛物线y2=4x的焦点,则该直线的倾斜角为( )
| A. | 0 | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
18.在长为12cm的线段AB上任取一点M,并且以线段AM为边作正方形,则这正方形的面积介于36cm2与81cm2之间的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{4}{27}$ | D. | $\frac{12}{45}$ |
12.已知球的半径为4,则这个球的表面积是( )
| A. | 32π | B. | 40π | C. | 64π | D. | 72π |
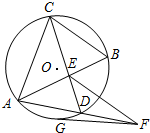 如图,已知圆O的两弦AB和CD相交于点E,FG是圆O的切线,G为切点,EF=FG.
如图,已知圆O的两弦AB和CD相交于点E,FG是圆O的切线,G为切点,EF=FG.