题目内容
【题目】已知函数![]() .
.
(1)设![]() ,求函数
,求函数![]() 的单调增区间;
的单调增区间;
(2)设![]() ,求证:存在唯一的
,求证:存在唯一的![]() ,使得函数
,使得函数![]() 的图象在点
的图象在点![]() 处的切线l与函数
处的切线l与函数![]() 的图象也相切;
的图象也相切;
(3)求证:对任意给定的正数a,总存在正数x,使得不等式![]() 成立.
成立.
【答案】(1)![]() 的单调增区间为(0,
的单调增区间为(0,![]() ];(2)证明见解析;(3)证明见解析.
];(2)证明见解析;(3)证明见解析.
【解析】
(1)求出导函数![]() ,在函数定义域内由
,在函数定义域内由![]() 确定其增区间;
确定其增区间;
(2)先求出![]() 在
在![]() 处的切线方程,设这条切线与
处的切线方程,设这条切线与![]() 的图象切于点
的图象切于点![]() ,由
,由![]() ,得出关于
,得出关于![]() 的方程,然后证明此方程的解在
的方程,然后证明此方程的解在![]() 上存在且唯一.
上存在且唯一.
(3)把问题转化为![]() 在
在![]() 上有解,令
上有解,令![]() ,则只要
,则只要![]() 即可.
即可.
(1)h(x)=g(x)﹣x2=lnx﹣x2,x∈(0,+∞).
令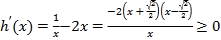 ,
,
解得![]() .
.
∴函数h(x)的单调增区间为(0,![]() ].
].
(2)证明:设x0>1,![]() ,可得切线斜率
,可得切线斜率![]() ,
,
切线方程为:![]() .
.
假设此切线与曲线y=f(x)=ex相切于点B(x1,![]() ),f′(x)=ex.
),f′(x)=ex.
则k=![]() ,
,
∴![]() .
.
化为:x0lnx0﹣lnx0﹣x0-1=0,x0>1.
下面证明此方程在(1,+∞)上存在唯一解.
令u(x0)=x0lnx0﹣lnx0﹣x0-1,x0>1.
![]() ,在x0∈(1,+∞)上单调递增.
,在x0∈(1,+∞)上单调递增.
又u′(1)=-1,![]() ,
,
∴![]() 在
在![]() 上有唯一实数解
上有唯一实数解![]() ,
,
![]() ,
,![]() ,
,![]() 递减,
递减,
![]() 时,
时,![]() ,
,![]() 递增,
递增,
而![]() ,∴
,∴![]() 在
在![]() 上无解,
上无解,
而![]() ,∴
,∴![]() 在
在![]() 上有唯一解.
上有唯一解.
∴方程![]() 在(1,+∞)上存在唯一解.
在(1,+∞)上存在唯一解.
即:存在唯一的x0,使得函数y=g(x)的图象在点A(x0,g(x0))处的切线l与函数y=f(x)的图象也相切.
(3)证明:![]() ,
,
令v(x)=ex﹣x﹣1,x>0.
∴v′(x)=ex﹣1>0,
∴函数v(x)在x∈(0,+∞)上单调递增,
∴v(x)>v(0)=0.
∴![]() ,
,
∴不等式![]() ,a>0ex﹣x﹣1﹣ax<0,
,a>0ex﹣x﹣1﹣ax<0,
即H(x)=ex﹣x﹣1﹣ax<0,
由对任意给定的正数a,总存在正数x,使得不等式![]() 成立H(x)min<0.
成立H(x)min<0.
H(x)=ex﹣x﹣1﹣ax,a,x∈(0,+∞).
H′(x)=ex﹣1﹣a,令ex﹣1﹣a=0,
解得x=![]() >0,
>0,
函数H(x)在区间(0,![]() )上单调递减,在区间(
)上单调递减,在区间(![]() ,+∞)上单调递增.
,+∞)上单调递增.
∵H(0)=0,∴![]() .
.
∴存在对任意给定的正数a,总存在正数x,使得不等式![]() 成立.
成立.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案【题目】某种植基地将编号分别为1,2,3,4,5,6的六个不同品种的马铃薯种在如图所示的
A | B | C | D | E | F |
这六块实验田上进行对比试验,要求这六块实验田分别种植不同品种的马铃薯,若种植时要求编号1,3,5的三个品种的马铃薯中至少有两个相邻,且2号品种的马铃薯不能种植在A、F这两块实验田上,则不同的种植方法有 ( )
A. 360种 B. 432种 C. 456种 D. 480种