题目内容
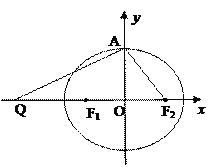
【题目】在极坐标系中，直线l：
，P为直线l上一点，且点P在极轴上方
以OP为一边作正三角形
逆时针方向
，且
面积为
．
求Q点的极坐标；
求外接圆的极坐标方程，并判断直线l与外接圆的位置关系．
【答案】（1）
；（2）直线与圆相外切．
【解析】
直接利用转换关系，把参数方程直角坐标方程和极坐标方程之间进行转换．
利用一元二次方程根和系数的关系求出结果．
由题意，直线l：
，以OP为一边作正三角形
逆时针方向
，
设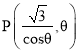
，由且
面积为
，则：
，得
，所以
.
由于为正三角形，所以：OQ的极角为
，且
，所以
由于为正三角形，得到其外接圆的直径
，
设
为外接圆上任意一点．
在
中，
，所以满足
．
故的外接圆方程，
又由直线l：
和的外接圆直角坐标方程为
．
可得圆心到直线的距离
，即为半径，故直线与圆相外切．
练习册系列答案
名校课堂系列答案
相关题目
