题目内容
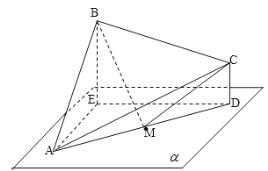
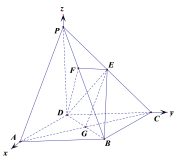
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,侧棱
是矩形,侧棱![]() 底面
底面![]() ,且
,且![]() ,过棱
,过棱![]() 的中点
的中点![]() ,作
,作![]() 交
交![]() 于点
于点![]() .
.
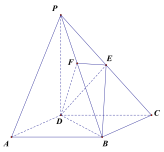
(1)证明:![]() 平面
平面![]() ;
;
(2)若面![]() 与面
与面![]() 所成二面角的大小为
所成二面角的大小为![]() ,求
,求![]() 与面
与面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)连接![]() 交
交![]() 于
于![]() ,则
,则![]() 是
是![]() 的中点,连接
的中点,连接![]() ,证明
,证明![]() ,
,![]() 平面
平面![]() 即得证;(2)如图以
即得证;(2)如图以![]() 为原点,
为原点,![]() 方向分别为
方向分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴正半轴建立空间直角坐标系.设
轴正半轴建立空间直角坐标系.设![]() ,根据面
,根据面![]() 与面
与面![]() 所成二面角的大小为
所成二面角的大小为![]() 求出
求出![]() ,再求出
,再求出![]() 与面
与面![]() 所成角的正弦值.
所成角的正弦值.
(1)证明:连接![]() 交
交![]() 于
于![]() ,则
,则![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,
则![]() 是
是![]() 的中位线,所以
的中位线,所以![]() ,
,
有因为![]() ,
,
所以![]() 平面
平面![]() .
.
(2)如图以![]() 为原点,
为原点,![]() 方向分别为
方向分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴正半轴建立空间直角坐标系.设
轴正半轴建立空间直角坐标系.设![]() ,则
,则
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,设
,设![]() ,则
,则![]() ,
,![]()
又![]() ,即
,即![]() ,解得
,解得![]() ①
①
设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则
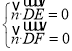 即
即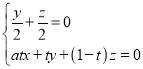 ,方程的一组解为
,方程的一组解为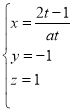 ,
,
显然![]() 是面
是面![]() 的一个法向量,依题意有
的一个法向量,依题意有
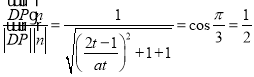 ,得
,得![]() ,
,
结合①式得![]() .
.
因为![]() 底面
底面![]() ,所以
,所以![]() 是
是![]() 与面
与面![]() 所成的角,
所成的角,
所以![]() .
.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目