题目内容
【题目】已知函数![]() 的定义域为
的定义域为![]()
(1)当![]() 时,求函数
时,求函数![]() 的单调递减区间.
的单调递减区间.
(2)若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)令f![]() (x)<0解得0<x<
(x)<0解得0<x<![]() 或
或![]() 得
得![]() 的单调区间.(2)法一:令g(x)=f(x)-1+sinx+
的单调区间.(2)法一:令g(x)=f(x)-1+sinx+![]() <0在
<0在![]() 上恒成立,利用g(
上恒成立,利用g(![]() )<0,求出a<-1,再对a<-1进行分类讨论.法二:变量分离,当x=0时,不等式恒成立;当
)<0,求出a<-1,再对a<-1进行分类讨论.法二:变量分离,当x=0时,不等式恒成立;当![]()
![]() ,再构造新函数,求最值即可.
,再构造新函数,求最值即可.
(1)![]() 时
时 ![]() ,
,![]()
![]() ,解得
,解得![]() 或
或![]()
所以函数的单调递减区间是![]() ,
,![]()
(2)方法一
![]() ,
,
则只需![]() 在
在![]() 时恒成立,
时恒成立,
则![]() 所以
所以![]()
![]()
因为![]() ,所以
,所以![]()
1)当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,![]() ,符合题意
,符合题意
2)当![]() 时,存在
时,存在![]() ,
,![]() 使得
使得![]() ,
,
①![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,![]() ,符合题意;
,符合题意;
②![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,![]() 时
时![]() 取得最大值;
取得最大值;
因为![]() ,所以
,所以![]() 所以
所以
![]()
令![]() ,其中
,其中![]()
则![]() ,
,
![]() 单调递增,
单调递增,![]() ,所以
,所以![]() ,
,![]() 时
时![]() ,符合题意;
,符合题意;
③![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;![]() ,符合题意。
,符合题意。
所以![]() 的取值范围是
的取值范围是![]()
方法二:
![]() 即
即![]()
当![]() 时,不等式恒成立
时,不等式恒成立
当![]() 时,只需
时,只需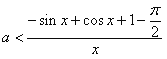 成立
成立
令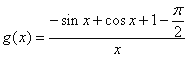 ,则
,则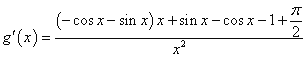
令![]()
则![]()
所以当![]() 时
时![]() ,
,![]() 单调递减
单调递减
当![]() 时
时![]() ,
,![]() 单调递增
单调递增
又因为![]() ,
,![]()
结合单调性可知![]() 时
时![]() ,
,![]() 时
时![]()
即![]() 时
时![]() 单调递减,
单调递减,![]()
![]() 单调递增。
单调递增。
![]() 时,
时,![]() 取得最小值
取得最小值![]()
所以![]() 的取值范围是
的取值范围是![]()

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目