题目内容
(本小题满分16分)
已知数列{an}的前n项和为Sn,且Sn=2an-2n+1,nÎN*.
(1)求数列{an}的通项公式;
(2)设bn= log2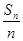 ,Tn=
,Tn=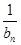 +
+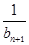 +
+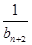 +…+
+…+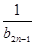 ,是否存在最大的正整数k,使得对于任意的正整数n,有Tn>
,是否存在最大的正整数k,使得对于任意的正整数n,有Tn>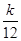 恒成立?若存在,求出k的值;若不存在,请说明理由.
恒成立?若存在,求出k的值;若不存在,请说明理由.
已知数列{an}的前n项和为Sn,且Sn=2an-2n+1,nÎN*.
(1)求数列{an}的通项公式;
(2)设bn= log2
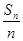 ,Tn=
,Tn=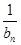 +
+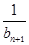 +
+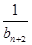 +…+
+…+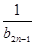 ,是否存在最大的正整数k,使得对于任意的正整数n,有Tn>
,是否存在最大的正整数k,使得对于任意的正整数n,有Tn>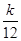 恒成立?若存在,求出k的值;若不存在,请说明理由.
恒成立?若存在,求出k的值;若不存在,请说明理由.(1)an=(n+1)2n,nÎN*.(2)存在最大正整数k=5,使得Tn>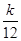 恒成立.
恒成立.
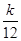 恒成立.
恒成立.本试题主要是考查了数列的前n项和与通项公式之间的互化问题,并能结合等差数列的定义得到通项公式,以及跟木同通项公式的特点,求解数列的和,采用了函数的单调性的思想,求解最值,从而得到常数k的值。
(1)根据已知的数列的前n项和与通项公式的关系,可以对于n=1,和n》2分为两种情况来分析得到结论。
(2)根据第一问中的通项公式,表示bn= log2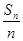 = n+1,和Tn,然后利用整体的单调性来求解参数k的值。
= n+1,和Tn,然后利用整体的单调性来求解参数k的值。
解: (1)当n=1时,a1=S1=2a1-22⇒a1=4; ·········· 1分
当n≥2时,an=Sn-Sn-1=(2an-2n+1)-(2a n-1-2n)⇒an- a n-1=2n,·········· 2分
⇒ -
-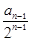 =1,且
=1,且 =2, ········ 3分
=2, ········ 3分
所以数列是以2为首项,1为公差的等差数列,
则 =2+(n-1)×1=" n" +1,所以an=(n+1)2n,nÎN*. ········ 6分
=2+(n-1)×1=" n" +1,所以an=(n+1)2n,nÎN*. ········ 6分
(2)由(1)得Sn=2an-2n+1=(n+1)2n+1-2n+1=n2n+1, ·········· 8分
则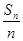 =2n+1,所以bn= log2
=2n+1,所以bn= log2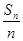 = n+1, ········ 10分
= n+1, ········ 10分
所以Tn=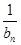 +
+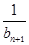 +
+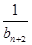 +…+
+…+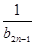 =
= 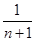 +
+ 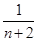 +
+  +…+
+…+ ,
,
Tn+1=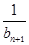 +
+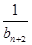 +
+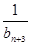 +…+
+…+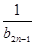 +
+ +
+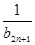 =
= 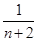 +
+ +
+ +…+
+…+ +
+ +
+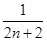 ,
,
Tn+1-Tn= +
+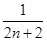 -
-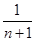 =
=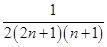 ,
,
又n是正整数,所以Tn+1-Tn=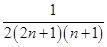 >0,即Tn+1>Tn,
>0,即Tn+1>Tn,
所以数列{Tn}是递增的数列,又T1 =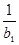 =
=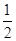 , ········ 14分
, ········ 14分
所以Tn≥T1=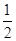 ,要使Tn>
,要使Tn>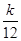 恒成立,只需
恒成立,只需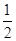 >
>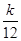 ,即k<6,
,即k<6,
又k是正整数,故存在最大正整数k=5,使得Tn>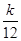 恒成立. 16分
恒成立. 16分
(1)根据已知的数列的前n项和与通项公式的关系,可以对于n=1,和n》2分为两种情况来分析得到结论。
(2)根据第一问中的通项公式,表示bn= log2
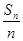 = n+1,和Tn,然后利用整体的单调性来求解参数k的值。
= n+1,和Tn,然后利用整体的单调性来求解参数k的值。解: (1)当n=1时,a1=S1=2a1-22⇒a1=4; ·········· 1分
当n≥2时,an=Sn-Sn-1=(2an-2n+1)-(2a n-1-2n)⇒an- a n-1=2n,·········· 2分
⇒
 -
-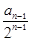 =1,且
=1,且 =2, ········ 3分
=2, ········ 3分所以数列是以2为首项,1为公差的等差数列,
则
 =2+(n-1)×1=" n" +1,所以an=(n+1)2n,nÎN*. ········ 6分
=2+(n-1)×1=" n" +1,所以an=(n+1)2n,nÎN*. ········ 6分(2)由(1)得Sn=2an-2n+1=(n+1)2n+1-2n+1=n2n+1, ·········· 8分
则
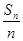 =2n+1,所以bn= log2
=2n+1,所以bn= log2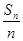 = n+1, ········ 10分
= n+1, ········ 10分所以Tn=
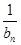 +
+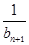 +
+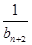 +…+
+…+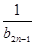 =
= 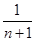 +
+ 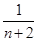 +
+  +…+
+…+ ,
,Tn+1=
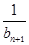 +
+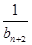 +
+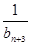 +…+
+…+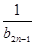 +
+ +
+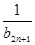 =
= 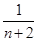 +
+ +
+ +…+
+…+ +
+ +
+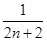 ,
,Tn+1-Tn=
 +
+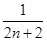 -
-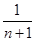 =
=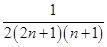 ,
,又n是正整数,所以Tn+1-Tn=
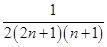 >0,即Tn+1>Tn,
>0,即Tn+1>Tn,所以数列{Tn}是递增的数列,又T1 =
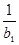 =
=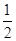 , ········ 14分
, ········ 14分所以Tn≥T1=
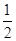 ,要使Tn>
,要使Tn>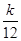 恒成立,只需
恒成立,只需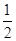 >
>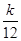 ,即k<6,
,即k<6,又k是正整数,故存在最大正整数k=5,使得Tn>
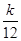 恒成立. 16分
恒成立. 16分
练习册系列答案
相关题目
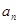 }中,
}中,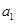 =3,其前
=3,其前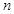 项和为
项和为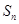 ,等比数列{
,等比数列{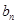 }的各项均为正数,
}的各项均为正数,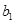 =1,公比为q,且b2+ S2=12,
=1,公比为q,且b2+ S2=12,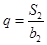 .
.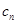 }满足
}满足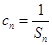 ,求{
,求{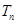 .
.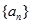 的首项
的首项 及公差
及公差 都是整数,前
都是整数,前 项和为
项和为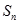 ,若
,若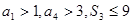 ,设
,设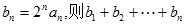 的结果为 。
的结果为 。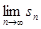 .
.
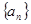 是等差数列,
是等差数列,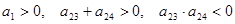 ,则使前
,则使前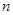 项和
项和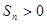 成立的最大正数
成立的最大正数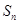 是等差数列
是等差数列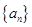 的前
的前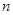 项和,已知
项和,已知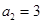 ,
,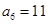 ,则
,则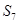 等于( )
等于( )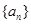 中,
中,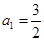 ,
,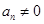 ,且
,且 ,则
,则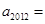 ___
___ 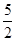
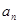 }的前n项和为
}的前n项和为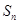 ,若
,若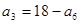 ,则
,则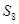 = ( )
= ( )