题目内容
等比数列{an}的前n项的和为Sn,已知S1,S3,S2成等差数列.
(1)求{an}的公比q;
(2)若a1-a3=3,求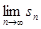 .
.
(1)求{an}的公比q;
(2)若a1-a3=3,求
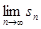 .
.
(1)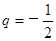 ;(2)
;(2)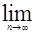
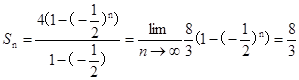
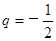 ;(2)
;(2)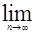
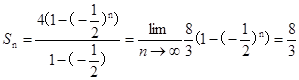
(1)本小题再利用S1,S3,S2成等差数列条件时,不直接利用前n项和公式而是转化为 ,这样可以避开对公比q是否为1的讨论。(II)在(I)的基础上利用a1-a3=3,可求出首项,进而可得到此数列是一个无穷等比递缩数列,所以其极根为
,这样可以避开对公比q是否为1的讨论。(II)在(I)的基础上利用a1-a3=3,可求出首项,进而可得到此数列是一个无穷等比递缩数列,所以其极根为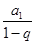 .
.
解:(Ⅰ)依题意有
由于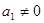 ,故
,故
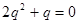
又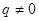 ,从而
,从而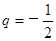 6分
6分
(Ⅱ)由已知可得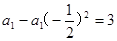
故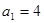 9分
9分
从而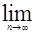
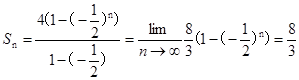 12分
12分
 ,这样可以避开对公比q是否为1的讨论。(II)在(I)的基础上利用a1-a3=3,可求出首项,进而可得到此数列是一个无穷等比递缩数列,所以其极根为
,这样可以避开对公比q是否为1的讨论。(II)在(I)的基础上利用a1-a3=3,可求出首项,进而可得到此数列是一个无穷等比递缩数列,所以其极根为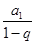 .
.解:(Ⅰ)依题意有

由于
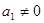 ,故
,故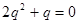
又
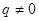 ,从而
,从而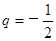 6分
6分(Ⅱ)由已知可得
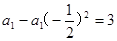
故
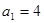 9分
9分从而
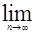
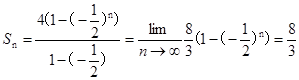 12分
12分
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
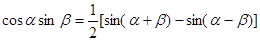 ;
; ,其中
,其中 ,其前
,其前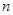 项和为
项和为 ,
,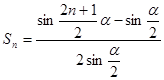 .
.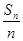 ,Tn=
,Tn=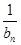 +
+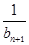 +
+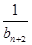 +…+
+…+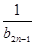 ,是否存在最大的正整数k,使得对于任意的正整数n,有Tn>
,是否存在最大的正整数k,使得对于任意的正整数n,有Tn>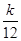 恒成立?若存在,求出k的值;若不存在,请说明理由.
恒成立?若存在,求出k的值;若不存在,请说明理由.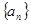 的前
的前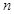 项和为
项和为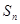 ,
,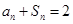 ,求
,求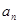 ;
;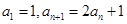 ,求
,求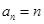 ,把数列
,把数列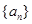 的各项排列成如下的三角形状:
的各项排列成如下的三角形状: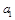


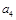
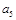
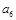
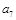


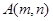 表示第
表示第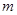 行的第
行的第 个数,则
个数,则 .
.  }的首项
}的首项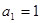 ,
, ,则下列结论正确的是( )
,则下列结论正确的是( )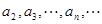 是等比数列
是等比数列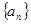 中,已知
中,已知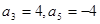 ,则
,则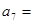 .
.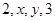 为等差数列,数列2,m,n,3为等比数列,则x+y+mn的值为( )
为等差数列,数列2,m,n,3为等比数列,则x+y+mn的值为( )