题目内容
18.已知函数f(x)=2x3+(4+$\frac{m}{2}$)x2-8x-16,对于任意的t∈[1,2],函数f(x)在区间(t,3)上不单调,则实数m的取值范围是( )| A. | (-$\frac{70}{3}$,+∞) | B. | (16,+∞) | C. | (-$\frac{70}{3}$,16) | D. | (-$\frac{70}{4}$,-16) |
分析 先求出函数f(x)的导数,问题转化为:$\left\{\begin{array}{l}{f′(t)<0}\\{f′(3)>0}\end{array}\right.$,解出即可.
解答 解:由函数f(x)=2x3+(4+$\frac{m}{2}$)x2-8x,
得:f′(x)=6x2+(8+m)x-8.
要使对于任意的t∈[1,2],函数f(x)在区间(t,3)上不单调,
说明导函数f′(x)的值在(t,3)上有正有负,
因为二次函数f′(x)=6x2+(8+m)x-8的图象开口向上,且恒过定点(0,-8),
所以,只需$\left\{\begin{array}{l}{f′(t)<0}\\{f′(3)>0}\end{array}\right.$,即:$\left\{\begin{array}{l}{{6t}^{2}+(8+m)t-8<0,①}\\{54+3(m+8)-8>0,②}\end{array}\right.$
由①得:m<-6t+$\frac{8}{t}$-8,(t∈[1,2],
而${(-6t+\frac{8}{t}-8)}_{min}$=-6×2+$\frac{8}{2}$-8=-16,
所以,m<-16.
由②得:m>-$\frac{70}{3}$.
综上:-$\frac{70}{3}$<m<-16.
故选:C.
点评 本题考察了函数的单调性,考察导数的应用,根据导函数f′(x)的值在(t,3)上有正有负,得到不等式组是解题的关键,本题是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知函数f(x)=$\left\{\begin{array}{l}|x+1|,-7≤x≤0\\ 1nx,{e^{-2}}≤x≤e\end{array}$,g(x)=x2-2x,设a为实数,若存在实数m,使f(m)-2g(a)=0,则实数a的取值范围为( )
| A. | [-1,+∞) | B. | (-∞,-1]∪[3,+∞) | C. | [-1,3] | D. | (-∞,3] |
9.设函数f(x)满足f(x)=f(4-x)(x∈R),且当x>2时f(x)为增函数,记a=f(1.10.5),b=f(0.51.1),c=f(log0.5$\frac{1}{16}$),则a、b、c的大小关系为( )
| A. | c<b<a | B. | c<a<b | C. | b<a,c | D. | a<b<c |
7.已知函数f(x)=$\frac{1}{1-x}$,g(x)=lnx,x0是函数h(x)=f(x)+g(x)的一个零点,若x1∈(1,x0),x2∈(x0,+∞),则( )
| A. | h(x1)<0,h(x2)<0 | B. | h(x1)>0,h(x2)>0 | C. | h(x1)>0,h(x2)<0 | D. | h(x1)<0,h(x2)>0 |
16.函数y=4sin(ωx+$\frac{π}{4}$)cos(ωx-$\frac{π}{4}$)-2sin(ωx-$\frac{π}{4}$)•cos(ωx+$\frac{π}{4}$)(ω>0)的图象与直线y=3在y轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,P4…,且|P3P5|=$\frac{π}{2}$,则此函数的递增区间为( )
| A. | [2kπ-$\frac{π}{2}$,2kπ+$\frac{π}{2}$](k∈Z) | B. | [$\frac{kπ}{2}$-$\frac{π}{8}$,$\frac{kπ}{2}$+$\frac{π}{8}$](k∈Z) | ||
| C. | [kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$](k∈Z) | D. | [$\frac{kπ}{2}$,$\frac{kπ}{2}$+$\frac{π}{4}$](k∈Z) |
 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且过点($\sqrt{3}$,$\frac{1}{2}$).
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且过点($\sqrt{3}$,$\frac{1}{2}$).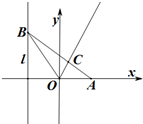 如图,已知定点A(1,0),点B是定直线l:x=-1上的动点,∠BOA的角平分线交AB于C.
如图,已知定点A(1,0),点B是定直线l:x=-1上的动点,∠BOA的角平分线交AB于C.