题目内容
6.已知函数f(x)=loga$\frac{1-mx}{x-1}$(a>0,且a≠1,m≠1)是奇函数.(1)求实数m的值;
(2)探究函数f(x)在(1,+∞)上的单调性;
(3)若a=2,试求函数f(x)在[3,5]上的值域.
分析 (1)由f(-x)=-f(x)得出loga$\frac{1+mx}{-x-1}$=-loga$\frac{1-mx}{x-1}$=loga$\frac{x-1}{1-mx}$,化简得$\frac{1+mx}{-x-1}$=$\frac{x-1}{1-mx}$,解出即可;
(2)利用复合函数的单调性讨论得出结论.
(3)由第(2)问结论利用单调性求出最值.
解答 解:(1)∵f(x)=loga$\frac{1-mx}{x-1}$(a>0,且a≠1,m≠1)是奇函数
∴f(-x)=-f(x),
即loga$\frac{1+mx}{-x-1}$=-loga$\frac{1-mx}{x-1}$.
∴loga$\frac{1+mx}{-x-1}$=loga$\frac{x-1}{1-mx}$
∴$\frac{1+mx}{-x-1}$=$\frac{x-1}{1-mx}$,
∴m=-1;
(2)f(x)=loga$\frac{1+x}{x-1}$=loga(1+$\frac{2}{x-1}$)
令g(x)=1+$\frac{2}{x-1}$,g′(x)=-$\frac{2}{(x-1)^{2}}$<0,
∴g(x)=1+$\frac{2}{x-1}$在(1,+∞)上是减函数.
∴当a>1时,f(x)在(1,+∞)上是减函数;
当0<a<1时,f(x)在(1,+∞)上是增函数.
(3)由(2)知当a=2时,f(x)在[3,5]上为减函数.
∴fmin(x)=f(5)=log2$\frac{3}{2}$,
fmax(x)=f(3)=log22=1.
∴f(x)在[3,5]上的值域是[log2$\frac{3}{2}$,1].
点评 本题考查了奇函数的定义,复合函数的单调性及函数单调性的应用.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
14.如果a,b,c∈R,那么“b2>4ac”是“方程ax2+bx+c=0有两个不等实根”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.已知角α的终边经过点P(-1,3),则2sinα+cosα=( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $-\frac{7\sqrt{10}}{10}$ | D. | $-\frac{\sqrt{10}}{2}$ |
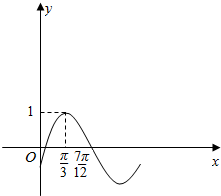 函数f(x)=sin(ωx+φ)(ω>0.|φ|<$\frac{π}{2}$)的图象部分如图所示.
函数f(x)=sin(ωx+φ)(ω>0.|φ|<$\frac{π}{2}$)的图象部分如图所示.