题目内容
已知数列{bn}是等差数列, b1="1," b1+b2+b3+…+b10=100.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)设数列{an}的通项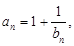 记Tn是数列{an}的前n项之积,即Tn= b1·b 2·b 3…bn,试证明:
记Tn是数列{an}的前n项之积,即Tn= b1·b 2·b 3…bn,试证明: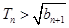
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)设数列{an}的通项
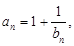 记Tn是数列{an}的前n项之积,即Tn= b1·b 2·b 3…bn,试证明:
记Tn是数列{an}的前n项之积,即Tn= b1·b 2·b 3…bn,试证明: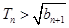
Ⅰ)设等差数列{bn}的公差为d,则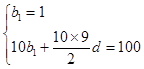 ,得d=2,
,得d=2,
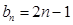 ……………………………2分
……………………………2分
(Ⅱ)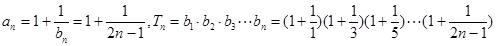
 ,命题得证 …4分
,命题得证 …4分
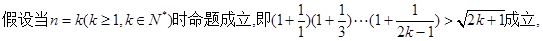
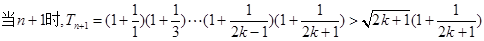
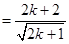
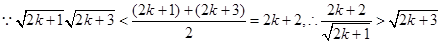 ……………10分
……………10分
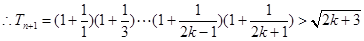
即n=k+1时命题成立
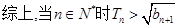
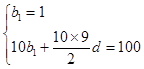 ,得d=2,
,得d=2,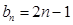 ……………………………2分
……………………………2分(Ⅱ)
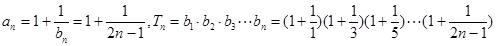
 ,命题得证 …4分
,命题得证 …4分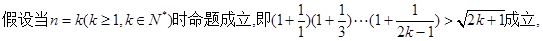
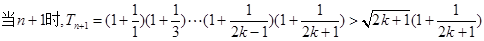
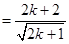
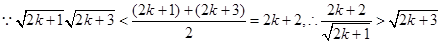 ……………10分
……………10分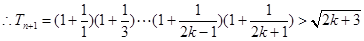
即n=k+1时命题成立
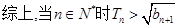
(1)根据等差数列求和公式求出公差,(2)求出Tn利用数学归纳法进行证明

练习册系列答案
相关题目
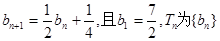 的前n项和。
的前n项和。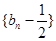 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式; 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。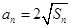 -1,
-1,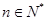 ,数列
,数列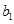 ,
,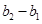 ,
,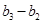 ……,
……,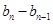 是首项为1,公比为
是首项为1,公比为 的等比数列。
的等比数列。 ,求数列{cn}的前n项和Tn。
,求数列{cn}的前n项和Tn。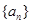 中,
中,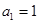 ,
,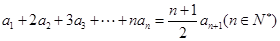
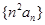 的前
的前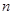 项和
项和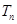 ;
;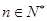 ,使得
,使得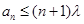 成立,求实数
成立,求实数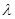 的最小值。
的最小值。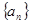 为等比数列,
为等比数列,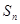 是它的前项和,若
是它的前项和,若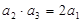 ,
,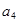 与
与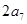 的等差中项为
的等差中项为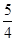 ,则
,则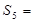 ( )
( )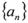 为等差数列,
为等差数列,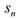 为其前n项和,且
为其前n项和,且 ,则
,则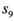 =
= ,a2+a5=4,an=33,则n为( )
,a2+a5=4,an=33,则n为( )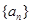 的前5项和
的前5项和 ,且
,且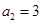 ,则
,则 ( )
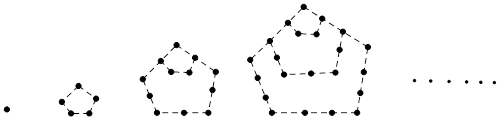
( )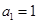 ,第2个五角形数记作
,第2个五角形数记作 ,第3个五角形数记作
,第3个五角形数记作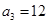 ,第4个五角形数记作
,第4个五角形数记作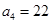 ,…,若按此规律继续下去,则
,…,若按此规律继续下去,则 ,若
,若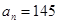 ,则
,则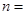 .
.